Testing regression coefficients

To test whether a regression coefficient is significantly different from zero is easy since this test is part of the output from Excel’s Regression data analysis tool or Real Statistics’ Multiple Linear Regression data analysis tool. E.g. for Example 2 of Multiple Regression Analysis in Excel, we see from Figure 3 of Multiple Regression Analysis in Excel that the coefficient for Infant Mortality is significantly different from zero, while the coefficient for White is not.

Test whether a regression coefficient equals a constant

It is pretty easy to test whether a regression coefficient is significantly different from any constant. E.g. for the multiple linear equation y = b₂x + b₁z + b₀ to test whether b₂ is significantly different from -1, you need to rewrite the regression equation as y+x = (b₂+1)x + b₁z + b₀. This equation can be represented as Y = B₂x + b₁z + b₀, which is a multiple regression model where Y = y+x the coefficient B₂ = b₂+1.

Note that b₂ = -1 when B₂ = b₂ – 1 = 0, and since we know how to test whether the B₂ coefficient is significantly different from zero, we have a test for whether b₂ is significantly different from -1.

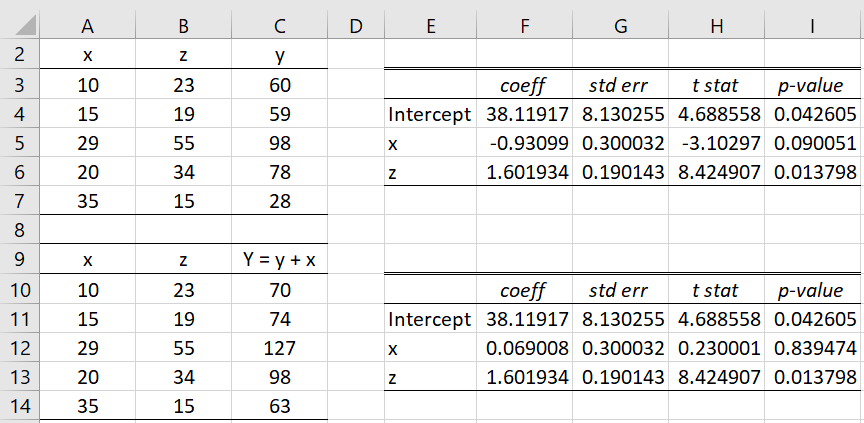
Example 1: Determine whether the x coefficient is significantly different from -1 for the linear regression model y = b₂x + b₁z + b₀ based on the data in range A2:C7 of Figure 1.

Figure 1 – Testing if x coefficient is significantly different from -1

We see from the regression analysis that the x coefficient is -.93099 (cell F5). From the revised regression analysis, based on the data in range A9:C14, we see that the x coefficient is .069008 with p-value = .85, indicating that coefficient B₂ is not significantly different from 0, and so b₂ is not significantly different from -1.

Test whether the intercept equals a constant

To test whether the intercept is equal to a specific constant is even easier. E.g. to test whether the constant for Example 1 is equal to 40, transform the regression equation to the equation (y-40) = b₂x + b₁z + (b₀-40), which takes the form Y = b₂x + b₁z + B₀ and test for B₀ = 0.

Test whether two coefficients are equal

You can use a slightly more complicated trick to test whether two regression coefficients are equal. To test whether b₂ is significantly different from b₁ in y = b₂x + b₁z + b₀, you need to rewrite the regression equation as y = B₂(x+z) + B₁(x-z) + b₀. Expanding the equation results in y = (B₁+B₂)x + (B₂–B₁)z + b₀, and so we see that b₂ = B₁+B₂ and b₁ = B₂–B₁. Thus, B₁ = (b₂–b₁)/2, which means that B₁ = 0 is equivalent to b₁ = b₂.

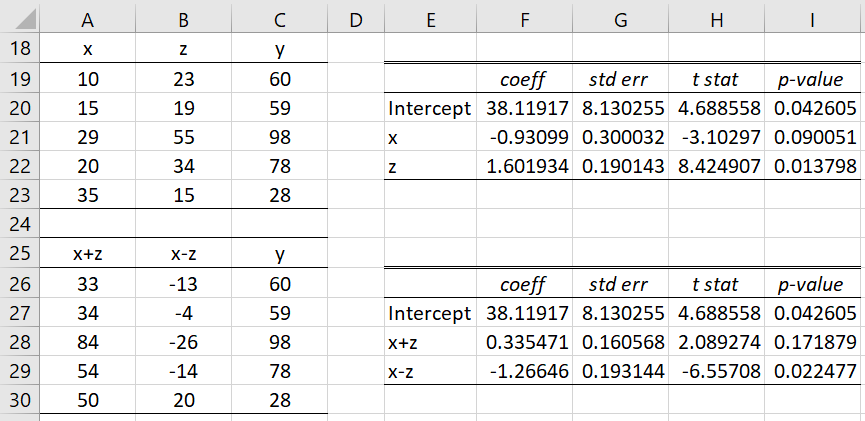
Example 2: Determine whether the x and z are significantly different for the linear regression model y = b₂x + b₁z + b₀ based on the data in range A2:C7 of Figure 1.

Figure 2 – Testing the equivalence of two coefficients

We see from the revised regression analysis that the p-value of the x-z coefficient is .02 (cell I29), which is a significant result. This indicates that the x and z coefficients in the original regression equation are significantly different.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Wheeler, A. P. (2016) Testing the equality of two regression coefficients
https://andrewpwheeler.com/2016/10/19/testing-the-equality-of-two-regression-coefficients/