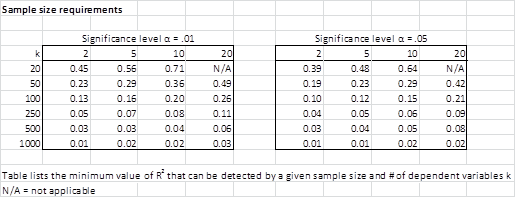
The table in Figure 1 summarizes the minimum sample size and value of R2 that is necessary for a significant fit for the regression model (with a power of at least 0.80) based on the given number of independent variables and value of α.
Figure 1 – Minimum sample size needed for regression model
E.g. with 5 independent variables and α = .05, a sample of 50 is sufficient to detect values of R2 ≥ 0.23.
With too small a sample, the model may overfit the data, meaning that it fits the sample data well, but does not generalize to the entire population.
Click here for more details about the minimum sample size required for regression.
Hello,
Thank you so much for your useful website.
I would be grateful if you help me.
I have 1 dependent variable with 4 independent variables. I have 10 data for each variable. I did multiple regression analyses and got good results. for example, the R square is 0.89 and the P-value for each variable is less than 0.05. I am not sure whether the sample size is small or not.
I greatly appreciate your guidance.
Best regards,
Maria,
I would consider a sample of 10 elements to be small, but it still can be big enough to achieve what you need.
E.g. if prior to performing your analysis, you want to determine whether a sample of size 10 is sufficient for regression with 4 independent variables where R-square >= .8 with power .80, then using Real Statistics’ Statistical Power and Sample Size data analysis tool you would find that the minimum sample size required is 10. If you wanted to achieve power of .90 then you would need a sample of size >= 11. If you only needed a model that was capable of achieving R-square = .85 then a sample of size 10 would be sufficient.
Charles
I got a data set which is less than 30yrs which is the normal threshold for good regression analysis, what should you do?
Hi Winnie,
It really depends on what you plan to use the regression analysis for, the number of independent variables you have, etc. This webpage gives some guidelines. It also provides a link for more detailed suggestions.
Charles
Hello Charles,
Can I run a Multiple Regression with the Stepwise Method in a sample of 21 participants? I have 1 dependent variable and 6 independent variables,
Hello Shouq,
That should work. I suggest that you try it and see what happens.
Charles
Hello Again,
Many thanks for your reply, this page is really helpful.
I just read through the questions here and I’m not sure if I can still run the Stepwise Multiple Regression, as my total sample = 21 participants and some of the variables have 19-20 participants due to missing data. and I have 1 normally distributed dependent variable and 6 independent variables. In case I can’t use Multiple Regression can I use Logistic regression and convert my continuous variables into binary or categorical?
Hello Shouq,
I would think that you would need to choose between multiple linear regression and logistic regression based on whether the dependent variable takes binary values rather than on sample size.
In any case, it is likely that llogistic regression will require a larger sample than multiple linear regression. See
https://web.pdx.edu/~newsomj/cdaclass/ho_sample%20size.pdf
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6422534/#:~:text=For%20observational%20studies%20with%20large%20population%20that%20involves%20logistic%20regression,parameters%20in%20the%20targeted%20population.
Charles
Dear Charles,
Thank you so much for your help and guidance,
I decided to perform a hierarchical regression model (to avoid some of the limitations of the stepwise method) but I’m confused about two things.
1/Which is the best order to enter my variables into the model?
Even though the total R square remains the same I noticed differences in the variables’ R square change (in the model summary table).
Are there any recommendations?
I tried to follow the stepwise method, where I entered the variables from the highly significant to the least significant.
2/ On what basis should I keep or remove a variable from the model? After the correlation step (All moderate to strongly correlate with the dependent variable r> 0.3), I checked the sig F change in the model summary table and the sig column and the Unstandardized B column in the coefficients table, Am I looking at the right output?
Dear Shouq,
I haven’t added support for hierarchical regression to Real Statistics yet, but I plan to do so shortly.
In the meantime, see https://library.virginia.edu/data/articles/hierarchical-linear-regression#:~:text=Hierarchical%20regression%20is%20a%20way,rather%20than%20a%20statistical%20method.
Charles
Hey Charles,
I really hope you can help me as I am pretty confused about how I should go about calculating the required sample size needed for my multiple regression to obtain a power of 80%.
In short, I ran a multiple regression to observe whether an individual’s sexual orientation (sex_orient) significantly impacted their life satisfaction (swls). Something like this: lm(swls ~ sex_orient + additional_predictor2 + additional_predictor3).
Importantly, this sex_orient variable was comprised of homosexuals and heterosexuals – it had two levels.
However, I had over 300 heterosexual respondents, but only 15 homosexual respondents, and thus concluded that my multiple regression was underpowered as a result of this low Homosexual sample size.
Therefore, I used the pwr.f2.test() function in Rstudio to calculate the required sample size to produce a power of 80% (as 80% is the minimum acceptable power).
Essentially, it stated that i needed a sample size of 37 participants for my multiple regression to have a power of 80%…BUT my issue is…is this 37 participants in EACH sexual orientation group OR just a sample of 37 participants, comprising of Homosexuals and Heterosexuals. I doubt it is the latter as this would not specify the ratio of Homosexuals to Heterosexuals.
So i was hoping you could help me find out how many Homosexual participants i would need in my sex_orient predictor variable for my multiple regression to obtain a power of 80%. It seems that this individual had the same issue: https://stats.stackexchange.com/questions/422834/multiple-regression-how-to-calculate-required-sample-sizes-for-individual-predi but unfortunately did not get a response.
Sorry for the long message, i hope i am making sense – if not, please do ask me to clarify.
Thanks!
Hello Ryan,
You raise an interesting question. If I look at the usual sample size analysis (e.g. from G*Power or R) the driver is the effect size (e.g. the expected R-square). If this split between Homosexuals and Heterosexuals directly impacts the effect size value, then the reported minimum sample size should be accurate. However, I don’t know how to translate this observation into a specific effect size.
Let me look at the problem in a different way. If you are doing regression and there is only one independent variable and it is sexual orientation, then regression is equivalent to a t-test (or ANOVA when there are more than two possible values). In this case, there are two samples size estimates, one for each of the two groups. In general, the sample size that matters the most is the size of the smaller group. If you have an additional categorical predictor, you can consider the regression to be two-factor ANOVA. With an additional continuous predictor, you have ANCOVA.
The sample size required depends on your objective. If you want to compare results based on sexual orientation, then I would imagine that a small sample of homosexuals could be a problem.
The only advice I could give is to try to map the regression model into one or more ANOVA (or t test) models (at least for the cases that you most care about) and see whether the sample size of 13 for the homosexual group is sufficient. If not then you need a bigger sample.
Charles
Hello, I’m conducting a power analysis and set my alpha level to .05, power to 80%, and I know the effect sizes for each one of my hypothesized effects from an existing dataset. Since I have multiple hypotheses (2 main effects and an interaction effect), should I be doing multiple power analyses to find estimated sample sizes for each hypothesized effect? If so, would I report the range of sample sizes from those power analyses or the largest sample size needed to detect an effect?
Hello Cait,
The effect size used is for the entire regression. See
https://www.real-statistics.com/multiple-regression/statistical-power-sample-size-multiple-regression/
For the 2 main effects and an interaction effect, you can estimate the sample size for ANOVA. See
https://www.real-statistics.com/one-way-analysis-of-variance-anova/power-for-one-way-anova/
https://www.real-statistics.com/one-way-analysis-of-variance-anova/power-tukey-hsd-test/
Since you have a two-way ANOVA, you can calculate 3 estimates for the sample size depending on which effect size that you use.
Charles
Hi Charles,
I have a total sample of 37 participants. I have three independent variables (IV). First IV has an overall score and five subscale scores. Second IV has an overall score only. Third IV has an overall score and three subscale scores. I have two dependent variables (DV). One DV has an overall score and three sub scale scores. Second DV has an overall score only. Would I be able to run a multiple linear regression meaningfully?
Thank you.
Hello Linda,
Do you plan to include the subscale scores in the model or just the overall score for each IV?
Recall that for Multiple linear regression there can be multiple IVs but just one DV.
See https://www.real-statistics.com/multiple-regression/multiple-regression-analysis/sample-size-multiple-regression/ for more information about how to calculate the sample size.
Charles
Hi Charles,
Thank you for your reply. I will be conducting a correlation analysis between the variables (including overall and subscales scores) to determine which scores I would be including in the model. I will be running two multiple regression, one for each DV.
Thank you.
Hi Linda,
Glad I could help.
Charles
Hi Charles, I am studying the impact of AI on recruitment and want to survey recruiters. My only criteria are that they are over 18 and work in recruitment (no restriction on location, age group, industry, etc.). What should be my optimum sample size with a Pearson α of 0.05, 7 Independent variables, and one dependent variable?
HU Abdullah,
To determine the sample size, you also need to specify the effect size (e.g. R-square) and power target (e.g. 90%).
E.g. to detect R-square >= .50 at power of 90% you need a sample of size 27 or more.
See https://www.real-statistics.com/multiple-regression/statistical-power-sample-size-multiple-regression/
Charles
Hello!
I have 20 people in my study (How does Hormone therapy affect Bone density and Body Fat%).
Now I want to look at how inital bodyfat % and duration of hormone therapy (months) affect the measured bodyfat % after at least 24 months of therapy.
First I did a paired t-test for the BF % and Bone density (which was also measured before and after therapy at the same time as BF) for the study population. Only BF% decreased significantly.
So I wanted to see how characteristics influenced the change of BF.
Independent variables:
1. Therapy duration in months( ranging from 24- 67 )
2. Initial measured BF% (18,7-39,8)
dependent variable:
1. BF% after 24 months of therapy.
In SPSS I did multiple regression. I believe I met all asumptions.
Results:
R squared= 0,453
Adj. R= 0,392
ANOVA Sig 0,004 ( p<0,05).
Coefficients:
HT Sig. 0,008
BF%1 Sig. 0,011
My Question:
Ist in meaningful to use multiple regression in this case?
I also played around with different diagrams, and could see that
1. the difference of BF% before and after HT was the greatest in the group of bigger fat percentage.
2. the biggest difference of BF% was seen in the groupes that had measurements between 2-3 years after started therapy.
It doesnt really matter that much for the dissertation, because the study has a lot of limitations. I simply find it really interesting and would like to understand a bit more.
Your help would be very appreciated!!
Thank you
Marie
I forgot to add. It puzzled me, I did a two way ANOVA.
I sorted HT duration into groups of year:
2-3(n=7)
3-4(n=7)
4-5(n=4)
5-6 (n=3)
I sorted body fat percentage into categories scores for the age group:
1. 16.6-19.4%(n=1)
2. 19.5-22.7% (n=5)
3. 22.8-27.1% (n=6)
4. >27.2 % (n=9)
However, HT duration and BF%1 are not significant, and dont interact.
Can the Two way ANOVA be not significant, but the ANOVA performed as a part of multiple regression be significant?
I am very sorry, if this is confusing. Thank you for your time and help.
Marie
Hello Marie,
Two-way ANOVA returns the significance for two factors along with the interaction between these factors. If you create the regression version of two-way ANOVA, the significance for the factors will be the same. Most likely the regression model that you created is not that model, and so it wouldn’t be surprising to see that the significance levels are different. You are probably comparing apples with oranges.
I would need to see your data, a clear statement of the hypotheses you are testing, and the results to be able to comment further.
Charles
Hi Marie,
Regression is typically used for these types of investigations. Even when you use ANOVA, under the covers it is regression.
Charles
Hi Charles,
Really helpful page!
I’m using 17 pp for my dissertation and wanted to use a multiple regression because I have 4 predictor variables (activity hours, optimism, specificity, sleep).
I ideally want to use this analysis but I’m not sure if I can as I don’t have many participants…
Can you help?
Hi Emma,
By 17 pp, do you mean 17 participants?
Charles
I think yes. I have the same case as Emma. In my research, there are only 16 participants and 4 independent variables. I want to use multiple regression to determine the effect. Is it possible? Thank you
You can certainly perform multiple regression. Since the sample size is small, you will be limited as to the effect that can be identified. This may not be a problem though. To get more information see the following webpage:
https://www.real-statistics.com/multiple-regression/statistical-power-sample-size-multiple-regression/
Charles
The population is 132, and i take 53 as a sample, and i use alpha level 5%, is my alpha level correct?
Generally, you choose your alpha value first (usually set to .05), the power objective (generally .80 or .90) and your effect size (R-square in this case). You then calculate the sample size needed.
Generally, the population size is not specified but is considered to be large.
In any case, without stating an effect size it is not possible to determine whether the alpha value is “correct”.
Charles
Hi,
I have a sample size of 26 and want to run multiple regression analysis with 1 dependent variable and 16 predicting/independent variables. Is that possible? Or is the sample size too small or are there too many predicting variables?
Thanks!
Hi Annelie,
You can certainly run such a multiple regression analysis. Whether or not this sample size is big enough to detect the desired effect depends on a number of factors, principally the alpha value, the desired power, the number of predicting variables and your estimate of the size of the effect that you need to determine. E.g. the smaller the effect the larger the sample. More information about this problem can be found at
https://www.real-statistics.com/multiple-regression/multiple-regression-analysis/sample-size-multiple-regression/
Charles
Thank you for the response!
I tried running the multiple regression analysis with the 16 predicting variables on 1 dependent variable for my sample of 26. I calculated the observed statistical power which was 0.158. I’m not sure, what does that tell me?
Hello Annelie,
Power of 0.158 is quite poor. It means that the sample size is inadequate. See the following for more details.
https://stats.idre.ucla.edu/other/gpower/multiple-regression-power-analysis/
Charles
Hello!
I have city tree data spanning from 2012 to 2020 and I want to do some ground truthing on the data to see if I can apply some allometry to it. Would there be a regression model that fits this scenario? I’m also curious to know what kind of sample size I would need for the ground truthing…
I think my independent variable is time, and my dependent variables are DBH (diameter at breast height) and height of the tree. There is only one inventory date per tree that basically states the DBH and height are true for that tree, that year.
Sorry in advance, stats is not easily understood for me
cheers!
Will
Hi Will,
I don’t completely understand the situation that you have described, especially since I don’t know anything about ground truthing or allometry.
What are you planning to use the regression model for? Which value(s) are you trying to predict?
If I represent your data as a matrix where each row has entries for time, DBH, height, then do I have only one row per tree or can I have multiple rows per tree? In fact, are all the rows about one tree or multiple trees?
Charles
hello good morning sir … i have 30 samples . dependent variable is crossbred cow rearing and independent variable like age, education, family type, access to market ..etc (10 independent variables) can i run multiple regression analysis or which tool i can use for it
You can certainly use multiple regression for such a situation. Which analysis is best depends on what you are trying to accomplish.
Charles
Hello I am working on data that has 301, and I want to decide whether I do listwise deletion or no, so I have multiple regression to examine the power of analysis. I run the analysis with 301 samples sizes with 11 independent variables and had given me an R2 of 0.056, but I am not sure if the sample size is enough or not.
Thank you!
See https://www.real-statistics.com/multiple-regression/statistical-power-sample-size-multiple-regression/
If you decide not to do listwise deletion, what would you do instead? You need to handle missing data in some way (e.g. via listwise deletion or imputation) in order to run regression analysis.
Charles
Hi! I am interested to know how many observations I need per category when I have a categorical predictor, such as sex. I can determine the overall required sample size, say 100, but what if I have 10 males and 90 females? Is that enough in each group to determine the predictive efficacy of the sex variable? hb
Howard,
See https://www.real-statistics.com/multiple-regression/statistical-power-sample-size-multiple-regression/
Charles
I want to run multiple regression analysis of 1 dependant variable against 16 independent variables for that how many sample I require ?
See https://www.real-statistics.com/multiple-regression/statistical-power-sample-size-multiple-regression/
Charles
Hi Charles!
I am conducting a multiple regression analysis with 36 sample size, how many independent variables can I use to have a good model. Thank you!
Hello Diane,
It depends on how you define a good model. I suggest that you look at the following webpage:
https://real-statistics.com/multiple-regression/statistical-power-sample-size-multiple-regression/
I suggest that you calculate the statistical power for different numbers of independent variables and see where the power remains above 80% (or 90% depending on your goal).
Charles
I have run the analysis with 36 samples sizes with 18 independent variables and had given me an R2 of 82%. And i have check the residual plot and showed random characteristics. But i worry how to verify the process how i chose the number of Independent variables. Thank you for reply!
With 18 independent variables, a sample of size 36 and alpha = .05, you will obtain power of 99.998% for R-square = .82.
Charles
Hi Charles! How can I determine the number of independent variables for only a sample
of 36 samples?
Diane,
What is a sample of 36 samples?
Charles
Hi Charles! I’m using 36 samples of number of occupants in 36 housing locations.
Also, a power of equally to 1, is it possible? or there is something wrong with the model.
Thanks
Diane,
No, this is not correct. With a sample of size 36, you can run a regression with a maximum of 33 independent variables.
With 27 variables, power is 95%. With 29 variables, power is 83%. With 33 variables, power is 24%
Hi Charles,
to add to my question posted on June 17th, since my study period is 30 years and no more then 30 observations of dependent variable are possible; therefore, 30 observations must be the entire population.
If it is the entire population, do I need to worry about having high p-values for the coefficients?
Do I need to worry about F-statistic?
To identify the best predictors, is it better to apply stepwise multiple regression or standard multiple regression with the Shapley-Owen decomposition?
Sorry for this flood of questions, but I am just getting my feet wet with statistics and find your explanations very clear and helpful.
Thank you,
Marzena
Hello Marzena,
Whether you need to worry about p-value or F-statistic really depends on what you want to do with the regression model. E.g. if you want to use the regression model to make predictions about a future dependent variable based on your estimates of the future dependent variables, then you don’t need to worry about the p-value. If you want to understand how accurate the prediction is then you need the p-value.
Stepwise regression, etc. are all methods for determining which dependent variables are most relevant for your regression model. Often it is more important, however, to use your domain knowledge (i.e. your understanding of the underlying scenario, not which variables are found to be most useful mathematically).
Charles
Hi Charles,
I want to run multiple regression analysis between 12 independent variables and one dependent variable. My sample size is 30, which in fact are all possible observations for the dependent variable (observations over 30 years, where only one observation per year is possible). Do I need to reduce the number of the predictor variables to 2 to comply with the rule of thumb of 15 observations per one independent variable?
The sample size requirement depends on a number of factors. With a sample of size 30 with 12 independent variables, as long as your expected R-square value is at least .60 you will achieve power of more than 95%. To detect an R-square of .3, however, you would need a sample of size 98.
Charles
Haii Charles,
I have a question about the minimum sample needed for me to conduct a reliable multiple regression. My population is 105 and I plan to have 35 sample size by using cluster sampling. Is 35 enough sample for F test to be significant? Thank you very much..
The website explains how to calculate the minimum sample size for regression using regular sample. Sorry, but it doesn’t yet explain issues related to cluster sampling.
Charles
Hi Charles,
Happy new year! I have proposed two independent variables, two dependent variables and one control variable for multiple regression analysis for my dissertation, what do you think will be my sample size? Do you have any reference(s) that I can use to justify it?
Thanks,
Teesco
Hi Teesco,
See the following webpage:
https://real-statistics.com/multiple-regression/statistical-power-sample-size-multiple-regression/
Charles
Hello Charles,
Thank you for providing the link. One more question; do you consider control variable as a predictor?
Teesco
Hello Teesco,
Based on your previous comment, I understand that you have two dependent variables plus a control variable. I assumed that the control variable was another dependent variable (and not a predictor), but you never stated this one way or the other. Also ordinary multiple regression assumes that there is only one dependent variable.
Charles
hello charles! I would like to some problems we encountered when we treat our data with multiple regression. The multiple r shows that there is no relationship between the independent variables and the dependent variable. While the p value of the one independent variable shows that there is a relationship. is there a case that it may happen , that there is a conflict between the dependent variable and independent variable
Joanne,
If you send me an Excel file with your data and analysis, I will try see what is going one.
Charles
Dear Charles,
Thank you very much for the explanation you have made. I want to clarify the following,
1. the p values for the variable coefficients are larger than 0.05, but the significant f value is less than 0.05. Does the model is a good model to interpret data?
Are you saying that the p-values for all the variable coefficients are larger than .05, yet the f value is significant? This should not happen. If you send me an Excel file with your data and output, I will try to figure out what has happened.
Charles
Hello again Charles,
I want to compare how students performed on a final exam for three independent groups of people (online, f2f and traditional) in order to see who did best.
2 of the setting data are approx. normal and the other left skewed.
Can I use the Mann Whitney U test to compare three settings? Any suggestions?
thanks!
Tonya,
Mann-Whitney works with two samples. You would need to use the test 3 times to get all 3 pairwise comparisons. This is acceptable provided you reduce alpha to account for the experiment-wise error rate — e.g. use .05/3, the Bonferroni correction. You can also use the Kruskal-Wallis test instead of ANOVA if the normality assumption is not met (assuming homogeneity of variances). These issues are all discussed in the ANOVA portion of the website.
Charles
Thanks again Charles:)
Charles. I took your advice and now have an additional question. I also realized I didn’t give you all the background so you can help me better. Sorry about that.
Brief background of setting: I have a blended, f2f and web course that all learned from diff. settings but took a very similar f2f final exam. The Web and Blended course data are normal (I used visual graphs and the Sharpiro Wilks test). The F2F data is definitely left skewed (not normal). Ultimately I wish to find out which setting performed better on the final.
Being that the Web and Blended data sets were normal and passed the homogeneity test, I ran a T-Test and it found that there is a difference in settings (P = .23, two tailed) so I declared the web setting performed better than the blended on the final b/c their mean and median scores were above the blended setting results.
Being that the f2f setting was not normal, I performed a Mann Whitney U test on the web/f2f (P=.508, two tailed) and blended/f2f (P=.282, two tailed). Both tested no difference in any of the settings. However, the results contradicted themselves. If the blended and f2F performed the same (or better yet, no difference was found) and the web and f2f, performed the same too,…how did the Web do better than Blended from the T-Test Results?
I also performed at Mann Whitney U on the Web/Blended too (I was just curious about how the results would go) and it yielded the same results at the T-Test. The p value was .018 which indicated there was a difference in the settings.
In your last correspondence with me, you suggested that I use a the Bonferroni correction of .05/3 (in my case). So my new significance level would be .017. With that being said, none of the test (T-Test and Mann U Test) p value is less than .017. Would I conclude that there is not any evidence to say one setting did better than the other ??? I am kind of weary of saying that b/c the T-Test (with normal) data should be believable right?
I’ve done A LOT of research before contacting you again and again. I need your advice once again. I can send you my SPSS outputs if you want to see them. However, I didn’t see an option to let me upload in this forum. Thanks for your help.
Tonya
Tonya,
First of all there is no contradiction. E.g. suppose that the means for the three groups Web, Blended and F2F are 3, 7, 5, respectively. Now suppose that a mean difference of 2 is not significant, but a mean difference of 4 is significant. This could represent your situation (over-simplified).
Now as for the Bonferroni correction. This is quite a conservative approach. It would be better to use ANOVA and then conduct one of the various post-hoc tests. The problem you have then is that the normality assumption for ANOVA is not met. You may be able to use Kruskal-Wallis in this case (a version of Mann-Whitney for more than 2 groups) and then follow up with one of the post hoc tests. See
https://real-statistics.com/one-way-analysis-of-variance-anova/kruskal-wallis-test/
https://real-statistics.com/one-way-analysis-of-variance-anova/kruskal-wallis-test/follow-up-tests-kruskal-wallis/
Charles
Thanks Charles,
Yes, I cannot do the One Way Anova b/c the F2f data is not normal. I ran the Kruskal-Wallis test and it showed no difference in the distribution of populations. The Ad Hoc found a sign diff between Web/Blended, not for Web/F2f or Blended/F2f. Should I conclude my results and say there was a sign found using the T-Test comparing the means of A and B but no evidence pointed significant difference in the means of A/C and B/C as per the Kruskal-Wallis test. Do you think it didn’t find any sign difference b/c of the sample size? Web (n=18), f2f (n=27) and blended (n=43)? Thanks again.
Tonya,
If the KW test showed no significant difference between the groups, you should stop there and not proceed to further tests.
I don’t know what you mean by “sign diff” using the t test.
Charles
Thanks, What I meant about the significance in the T-Test is that I performed a T-Test on the Blended and Web b/c those data were normal and it found a significant difference (rejected the null),..so I know I can conclude that for those 2 settings. But as for all three settings, I will accept that no difference was found in the data using Kruskal-Wallis Test.
Thanks so much again for your help:)
Hi Charles!
I wish to find out if there are differences in student achievement as measured by the course final grades (GPA) and final exam scores on whether a course was taught in an online, blended, or traditional format? If so, what are these differences? All of the three settings (web n=18 approx. normal, blended n=43 approx. normal, f2f n=27 left skewed) took the same final exam on campus f2f. A linear regression was done for the web and blended using SPSS which found a significant relationship between the GPA and final exam for both settings . However as for the constant term produced for the web (not the blended) in the coefficients table, the p value was greater than .05 (it was .063). The p value for the blended was < .05 (-0.00) so that was fine.
1) I did some research online and it was suggested to not use the linear model for the web setting b/c the constant produced is not significant. What are your thoughts?
2) Does that mean, I shouldn't trust all other SPSS results for the linear analysis for the web setting and just determine that the relationship between the GPA and Final was not significant.
3)As for the f2f settings which is left skewed,.. I did some research that suggested me using the boot strapping regression model in which produces a 95% confident interval that the coefficient for GPA final is between two values it will find for you after you preform the test. Any thoughts on this?
Lastly, I am now realizing that my sample size is probably too small to even trust these results. I don't know what to do now 🙁 I am very new at statistical analysis at this level. I learned it almost 10 years ago. I will appreciate any help you can give me. Thanks.
Tonya,
1) By constant, I assume that you mean the regression coefficient for the web setting variable. Whether you keep or remove this variable depends on what you plan to use the regression model for. You can remove the variable, but before you do you should rerun the regression analysis without this variable and make sure that the other two variables are still significant. This sort of decision making is discussed on the following webpage:
Stepwise Regression
2) You should still be able to trust the other SPSS results even if you retain the web setting variable, but you probably can remove it from the other analyses.
3) You can use regression for prediction even if one of the variables is skewed. The confidence intervals for the coefficients (and therefore for the predictions) won’t be accurate, but perhaps you are not interested in these. Bootstrapping is a good way to go when the assumptions are not met and the results that you are interested in depend on these assumptions.
4) Sample size requirements for regression are described at
https://real-statistics.com/multiple-regression/statistical-power-sample-size-multiple-regression/
Charles
Thank you very much!
Hello Charles,
I really appreciate your effort and it is very useful.
I have seen the figure 1 and according to that determined my sample size. I would be grateful if you can tell me the citation for this calculation. How i can cite it in my article.
Any Journal article or book?
Thank You
Mehwish,
I can’t remember where I found the original version of this table, but I calculated the latest version of the table myself using the Real Statistics Statistical Power and Sample Size data analysis tool (selecting the Regression and Sample Size options).
Charles
Dear Charles,
I have been trying the last period to calculate the sample size using a-priori Sample Size Calculator for Multiple Regression but when using this method I need to decide on the “Number of predictors” but i couldn’t do it as I have 6 independent variables and 1 dependent variable under each IV I have 1-2 dimensions and 2-3 questions with multiple choices? kindly advise what is the best way to calculate the number of predictors using a-priori Sample Size Calculator for Multiple Regression? For the effect size, I am planning to use the medium one as sensitivity is not need and the medium is commonly used. Please advise am I correct?
Your kind assistance is very much appreciated.
Bests,
Wafa
Dear Wafa,
With 6 independent variables and 1 dependent variable, there is no problem. Just use the approach described on the webpage.
But from your comment I understand that the complication is that the value of each independent variable depends on some other calculations (based on dimensions and number questions). This shouldn’t matter as long as you have a measurement for each independent variable.
If the approach that you use requires that you perform more than one regression, then situation changes. Depending on the details, perhaps you can calculate the sample size required fro each regression and take the largest of these sample sizes.
As far as the effect size, as long as you are satisfied that a medium-sized effect is sufficient, then go with the value for a medium-sized effect.
Charles
Dear Sir,
I have population of 650 and I will use multiple regression analysis. I got confused how I can do the sample size for this population. I kindly really need the steps to do . I have found many ways and I am very confused which one to use.
Wafa,
See https://real-statistics.com/multiple-regression/statistical-power-sample-size-multiple-regression/
Charles
Many Thanks for your kind and quick reply. It is very much appreciated.
I opened the link and it is very clear to me now. I kindly need a clarification : Is the calculation of R2 based of my choice of Cohen’s effect size (small, medium and large) or it is the other way around. I mean how I can calculate R2 if it is not based on f2?
Wafa,
It is a good question. If you have already done the multiple regression and want to calculate the power of the regression, then you can use the R-square value calculated by the regression. If you want to calculate how big a sample size that you need (a priori, i.e. before conducting the experiment) then things are more difficult. Since f-square can be calculated from R-square and vice versa, it is probably better to think in terms of how sensitive an analysis you need. The bigger the effect size you need to detect, the less sensitive the analysis and so the smaller the sample size required. On the other hand, if you want to detect a small effect then you will need a larger sample size.
Charles
Hello Charles,
I now started to read your website from start to finish :-), there are loads of concept that I never had time to really understand when doing my degree that are made very clear by your explanations.
Could you give me an example of when a small R^2 value would be considered interesting? Usually, I *think* I remember only considering models that explain a “large” part of the variance in the data (so f.i. R^2=80% was better than R^2=20%).
Many thanks!
Fred
Fred,
This really depends on your definition of “interesting”.
If the sample is sufficiently large, a linear regression model can yield a significant fit for the data even when it has a very small R-square value. Whether this is interesting or not really depends on your definition of “interesting”. Note that I am using the word “significant” in a precise statistical sense, while the word “interesting” doesn’t have a precise definition in this context.
We could also use words like “useful”, which I might use to mean that the predictions from the model are better than chance (or at least better than simply using the mean of the sample y data), although another person might choose to find such a model useful only when its accuracy is a lot better than chance.
Charles
Thanks Charles, it makes sense but doesn’t the Rsquare value represent by what percentage the variance in the y’s has been reduced by using linear regression?
So in your example, random would correspond to using the Grand Mean to predict a y given an x value.
In many cases using the value in the regression would improve that estimate as those values would on average be Closer to the observed values.
Thanks!
Fred,
R square represents the percentage of the variance captured by linear regression.
You clearly expect that the linear regression estimates would be closer to the observed values than the mean of the y values.
Charles
Good Day,
I am trying to vet a Linear Regression model that I am constructing based on what value of R2 is acceptable given my sample size and number of dep. variables. The table ‘Figure 1 – Minimum sample size needed for regression model’ is a great help although as this is an academic study I need to reference this table. Could you please provide the source of this table?
Michael,
Sorry, but I can’t recall where I got the table from, but in any case you can simply calculate the values in the table yourself by using the Real Statistics Statistical Power and Sample Size data analysis tool or the G*Power software. The numbers will be slightly different, but similar.
Charles
hello sir greetings,
I am doing a project on Pavement Deterioration modelling for which i am trying to use excell for the purpose of regression analysis of the data collected. I have 4 independent variables and a dependant variable. I tried to do regression analysis for the data but the result is unsatisfactory. the result page contains p-value”#NUM!”. What may be the reason for this and how may i solve this problem.
And when I do the same considering 2 independant variables, I am getting the results.
I need to use all the 4 independent variable, please help me out sir.
This probably indicates some anomaly in your data (too few samples, all the data for one group are identical, etc.). If you send me an Excel file with your data, I will try to figure out why you are getting a #NUM! value, See Contact Us for my email address.
Charles
What if the incidence rate of each variable k (e.g., mutation rate per gene) is very low, e.g., 1 in 100,000? Surely the sample size must take the incidence per variable into account, otherwise you would be evaluating correlations between mutations that never occur because the sample is too small.
Is there a general formula that links the probability p to the sample size n, correlation coefficient R^2, number of variables k and also the incidence rate f per variable?
Kelvin,
I suggest that you provide a specific example and let-s see what happens if we use the usual tests.
Charles
Hi Charles, many thanks for responding.
My question relates to fundamental theoretical limitations of Big Data in human genomics. Specifically, I am trying to determine the minimum sample size n required to identify a correlation between k binomial variables, where each variable occurs with incidence rate f. For example, how many patients do we need to study in order to find a correlation between k different genes, where each gene varies from the norm with frequency f?
What is the mathematical relationship (formula) between the p-value and the sample size n, number of genes k, the mutation rate per gene f, and the correlation coefficient R (or some other measure of effect size)?
I ask because the sample size calculation you show above does not take into account the frequency with which each individual gene may vary from the normal state.
Thanks for any guidance.
Kelvin
PS. To give a more concrete example, let’s say that we are looking for a correlation between 10 genes, where each gene is mutated at a frequency of only 1 in 100,000. How many patients do we need to identify a “significant” correlation between these 10 genes and a binary disease state?
Kelvin,
Let me try to understand the scenario you are painting. Once I capture the scenario properly it should be easier to address (or at least try to address) your question about sample size.
1. You have n patients
2. Each patient has k genes under study (these are the variables).
3. I am not sure what sort of values there are for the genes. Do these take values 0 and 1 or decimal values? How are these values distributed (via the normal distribution with an occasional mutation defined by f)? Is the norm known? Is the norm the same for each gene? Is the mutation rate the same for each gene?
4. I am not what the nature of f is. E.g. the value of each gene is 0 or 1, randomly distributed (50% 0 and 50% 1) but once every 100,000 patients with gene 0 the 0 is changed to 1. This probably not what you mean, but I need to have a clearer idea of how the mutation rate interacts with the distribution of the gene values.
Charles
Hi, Charles
Tried to find a function on your website that provided the ability to determine sample size for multiple regression where one could input the characteristics described on this page. If no function, is there, or could there be, a set of larger tables where one could make more refined extrapolations to determine sample size?
Thanks,
Rich
Rich,
Sorry that I haven’t gotten around to this sooner. I plan to add two new functions (REG_POWER and REG_SIZE) with this capability in the next few days.
Charles
Hi, Charles
Thanks for the new multiple regression calculators.
Perhaps, in the future, the example/discussion on this page can be used or expounded on in the new page that documents the new features availed in version 3.4.
Regards
Rich