Moderation Analysis

Moderation Analysis is used to determine how much the relationship between the independent (X) and dependent (Y) variables changes based on the addition of a moderating (M) variable.

The analysis is performed using linear regression using X, M, and X*M as independent variables and Y as the dependent variables. This analysis makes sense when there is a significant correlation between X and Y, but there isn’t a significant correlation between M and Y.

Before carrying out the regression, we first center the X and M (or optionally standardize these variables). This makes the interpretation easier and reduces multicollinearity.

Example

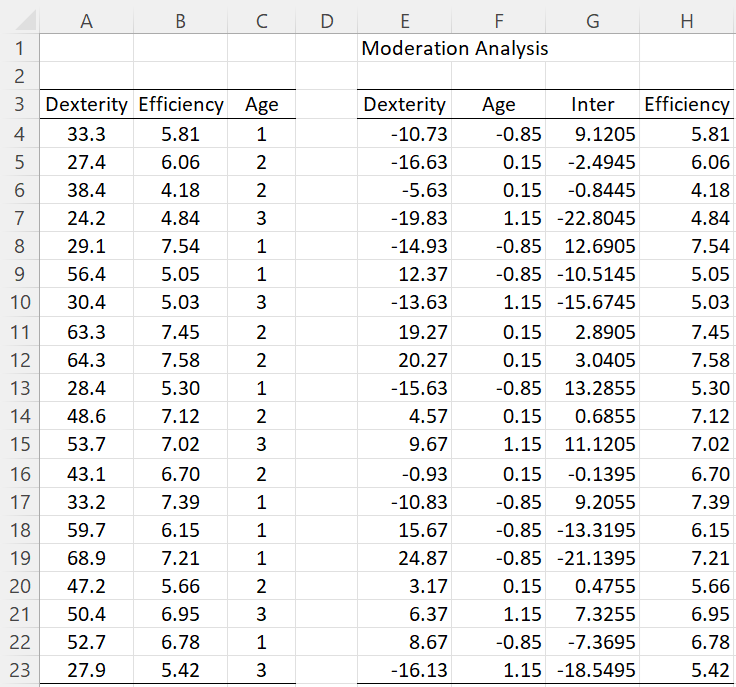
Example 1: Determine whether Age (M) has a moderating effect on the relationship between Dexterity (X) and Efficiency (Y) for operators in a chemical plant based on the data displayed on the left side of Figure 1.

The right side of the figure contains the centered data along with the interaction X*M. Here, range E4:E23 contains the array formula =A4:A23-AVERAGE(A4:A23) and F4:F23 contains =C4:C23-AVERAGE(C4:C23). Cell G4 contains the formula =E4*F4 and cell H4 contains =B4, and similarly for the other cells in columns G and H.

Figure 1 – Raw and centered data

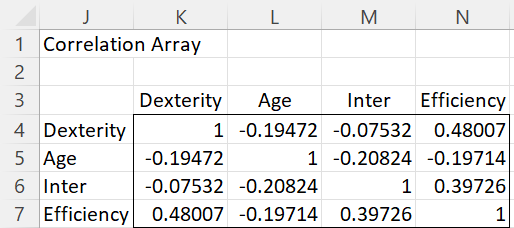
Correlations

It appears from Figure 2 that Dexterity (X) and Efficiency (Y) are correlated, while Age (M) and Efficiency (Y) are not correlated. Here, we placed the array formula =CORR(F4:H23) in range K4:N7.

In fact, if you ran the Correlation Test data analysis tool, you would see that the first correlation is significantly different from zero (p-value = .03), while the second is not significantly different from zero (p-value = .40). You will see similar results from the regression shown in Figure 3.

Figure 2 – Correlations between the variables

Regression

We now use the Regression data analysis tool using Dexterity, Age, and the Interaction between Dexterity and Age as the independent variables and Efficiency as the dependent variable. The result is shown in Figure 3.

Figure 3 – Regression analysis

We see from Figure 3 that the Interaction is significant (p-value = .04 in cell T20), which shows that Age has a moderating effect on the relationship between Dexterity and Efficiency. We see this more clearly in the Level Analysis shown in Figure 4.

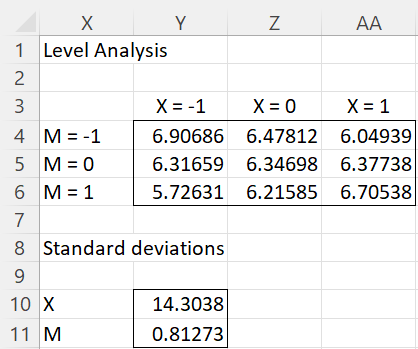
Level Analysis

This figure displays the predicted values for Efficiency (Y) using the usual formula

For values of Dexterity (X) at -1, 0, 1 standard deviations from the mean (which is now centered on zero) and -values of Age (M) at -1, 0, 1 standard deviations from its mean.

Figure 4 – Level analysis

Here, cell Y10 contains the standard deviation for X using the formula =STDEV.S(E4:E23), and Y11 contains the standard deviation for M using the formula =STDEV.S(F4:F23).

E.g. cell Y6 (where X = -1, i.e. one standard deviation below the mean, and M = 1, i.e. one standard deviation above its mean) contains the formula

using the worksheet formula =Q17-Q18*Y11+Q19*Y10-Q20*Y10*Y11.

Level Analysis Chart

The relationship is easier to see graphically, as shown in Figure 5.

Figure 5 – Level analysis chart

To create this chart, highlight range X4:AA6 and select Insert > Charts|Line Chart. After some fine-tuning, the result shown in Figure 5 appears.

X = -1 represents a low level of Dexterity, X = 0 represents a mean level of Dexterity and X = 1 represents a high level of Dexterity. M = -1, 0, 1 can be interpreted in a similar manner for Age (younger, mean, older). We see from the blue line in Figure 5 that for younger workers, perhaps counter-intuitively, higher levels of Dexterity result in lower Efficiency. For the mean-aged workers (the red line), higher levels of Dexterity result in slightly higher levels of Efficiency; while for older workers (grey line), higher levels of Dexterity result in higher levels of Efficiency.

Data Analysis Tool

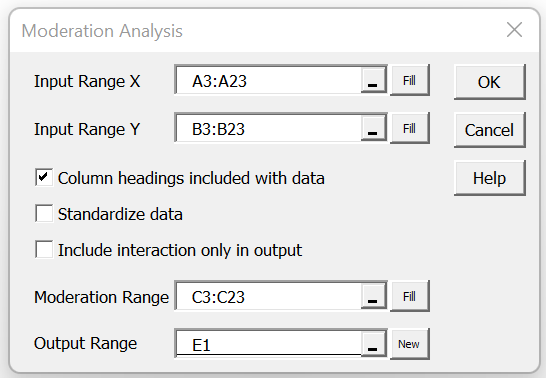
Real Statistics Data Analysis Tool: To perform the analysis for Example 1 using the Real Statistics Resource Pack, you can press Ctrl-m and select the Moderation Analysis option (from the Reg tab when using the multi-page user interface). Next, fill in the dialog box as shown in Figure 6.

Figure 6 – Moderation Analysis dialog box

When you click on the OK button, the output shown in Figures 1, 2, 3, 4, and 5 appear.

If you check the Standardize data option then the X and M input data will be standardized instead of centered. In this case, the standard deviations shown in Figure 4 won’t be displayed since they are both one.

You can optionally insert A3:B23 in the Input Range X field and leave the Input Range Y field empty to obtain the same result.

If you check the Include interaction only in output, then the independent variables for the regression will be the moderating variable (M) and the interaction, and not X. This is similar to the approach used by SPSS. In this case, the Level Analysis will not be included in the output.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Howell, D. C. (2010) Statistical methods for psychology (7^th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf

Wuensch, K. (2016) Continuous Moderator Variables in Multiple Regression Analysis
https://www.studocu.com/en-us/document/east-carolina-university/psychological-statistics/continuous-moderator-variables-in-multiple-regression-analysis/1068430

Memon, M. A., Cheah, J-H, Ramayah, T., Ting, H., Chuah, F. Cham, T. H. (2019) Moderation analysis: issues and guidelines. Journal of Applied Structural Equation Modeling
https://jasemjournal.com/wp-content/uploads/2019/10/2019-Memon-et-al-Moderation.pdf

Cucos, L. (2022) How To Perform Moderation Analysis in SPSS [2 Methods]. Uedufy
No longer available online

Edwards, J. R. (2008) Seven deadly myths of testing moderation in organizational research
https://psycnet.apa.org/record/2008-09949-006