Standard Errors of LAD Regression Coefficients via Bootstrapping

Procedure

In LAD Regression via Simplex Method and LAD Regression via IRLS we describe two approaches for calculating the LAD regression coefficients. We now show how to calculate the standard errors of these coefficients using bootstrapping. Bootstrapping is described in Resampling Procedures, but now we will define the approach for using bootstrapping to estimate the standard error of a parameter θ provided we have some methodology for creating an estimate θ-hat of θ based on a sample of size n.

1. Choose m sets T₁, …, T_m consisting of n elements chosen at random from the sample with replacement (these are the bootstraps).
2. For each T_i, calculate θ_i-hat in the same way as θ-hat was calculated using the pseudo-sample T_i
3. Calculate the mean of the θ_i-hat.
4. The bootstrap estimate of the standard error is the standard deviation of the θ_i-hat.

Note that the estimated standard errors will change based on the number of bootstraps (the value m above) and the specific random values in the T_i. This means that if you run this procedure twice, you are apt to get two different answers. Hopefully, setting m large enough will keep this variation to a minimum.

Of course, the larger the value of m, the more time it will take to complete the procedure. Since the calculation of the LAD regression coefficients using IRLS is already somewhat resource intensive, caution must be exercised to make sure that the processing time is not too long. We will use the default of m = 500, although for smaller samples, m = 2,000 is not too time-consuming.

Example

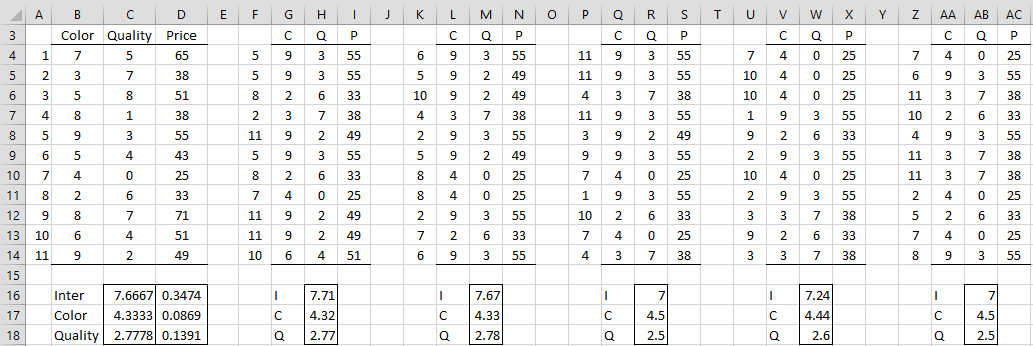
We show in Figure 1 how to calculate the standard error of the intercept, color and quality LAD regression coefficients for Example 1 of LAD Regression using IRLS (the data of which is replicated in Figure 1) using 5 bootstraps. Obviously, this number of bootstraps is too small, but it will illustrate the technique.

Figure 1 – Bootstrapping to find the standard errors

The first bootstrap is shown in columns F through I. The range F4:F14 is calculated using the array formula =RANDOMIZE($A4:$A14). The value in cell G4 is calculated by =INDEX(B$4:B$14,F4) and similarly for the other values in range G4:I14. The regression coefficients for the data in range G4:I14 are calculated using the array formula =LADRegCoeff(G4:H14,I4:I14) in range H16:H18.

The other four bootstraps are shown on the right side of Figure 1. The estimated standard error for the intercept coefficient is equal to the standard deviation of the five bootstrap intercept coefficients. This is shown in cell D16 as calculated by the formula =STDEV(H16,M16,R16,W16,AB16). The color and quality coefficient standard errors are calculated in a similar manner in cells D17 and D18.

Worksheet Function

Real Statistics Function: For the following array functions, R1 is an n × k array containing the X sample data, R2 is an n × 1 array containing the Y sample data, con = TRUE (default) if a constant term is included, iter is the number of iterations performed (default 25) and nboots = the number of bootstraps (default 500).

LADRegCoeffSE(R1, R2, con, iter, nboots) = column array consisting of the standard errors of the regression coefficients; if con = TRUE, then the output is a k+1 × 1 array, while if con = FALSE, it is a k × 1 array

For example, the output in range D16:D18 of Figure 1 could be obtained using the array formula =LADRegCoeffSE(B4:C14, D4:D14, TRUE, 25, 5).

References

Furno, M. (1998) Estimating the variance of the LAD regression coefficients. Computational Statistics and Data Analysis.

https://www.academia.edu/20240900/Estimating_the_variance_of_the_LAD_regression_coefficients