This test is similar to the Breusch-Pagan Test, except that in the second OLS regression, in addition to the variables x1, …, xk we also include the independent variables x12, …, xk2 as well as x1xj for all i ≠ j. This test takes the form
where m = the number of independent variables in the second regression, not counting the constant term. Thus m = 2k + C(k,2). The F statistic version of the test is
Because this test uses up a large number of the degrees of freedom (and so requires a large sample), we can instead use the secondary OLS regression of the sample residuals r2 on the values predicted by the first OLS regression y-hat along with y-hat squared and a constant. This test takes the form
or
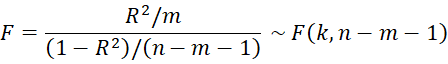
Example 1: Conduct the White test for the data in Example 1 of Breusch-Pagan Test.
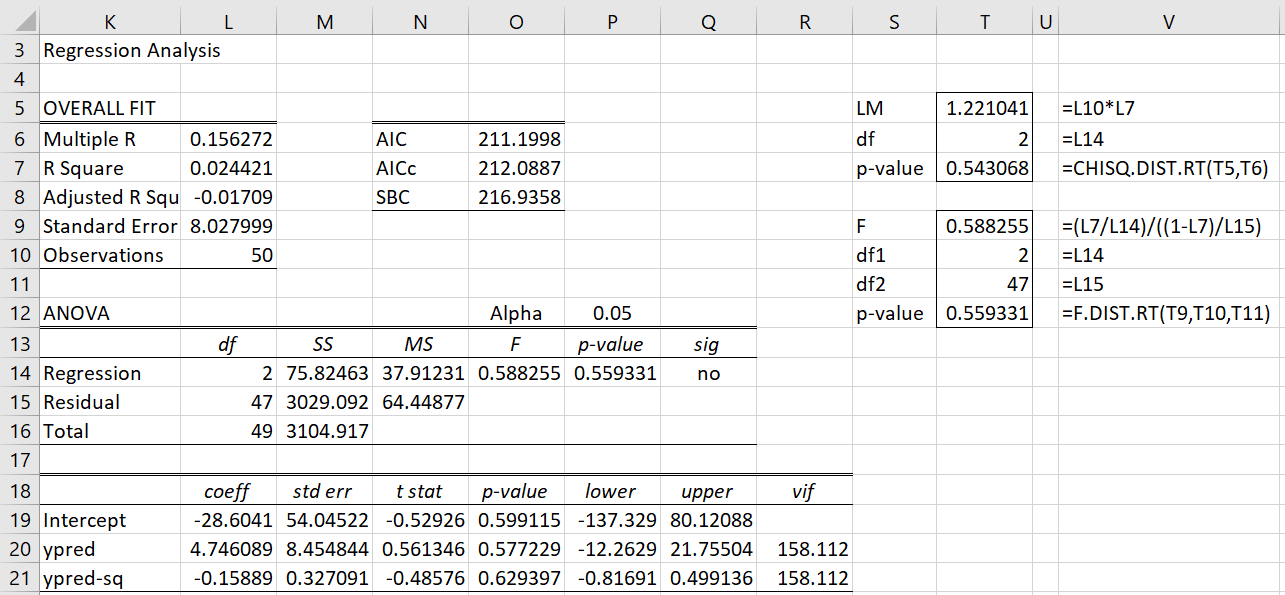
Figure 1 – Data for White Test
Figure 1 displays the data required for White’s test (only the first two of 50 rows is shown). The data is just like that shown on the right side of Figure 1 of Breusch-Pagan Test except that the square of the predicted value (column G) is also displayed.
We now carry out regression using columns F and G as the independent variables and column I as the dependent variable. The result is shown in Figure 2.
Figure 2 – White Test
With p-value = .54 and .56, once again we get evidence that there is no heteroskedasticity.
Real Statistics Functions: The following Real Statistics function automates the simpler version of the White test in Excel.
WhiteStat(R1, R2, chi) = White statistic for the X values in R1 and Y values in R2; if chi = TRUE (default) then LM statistic is returned; otherwise F statistic is returned.
WhiteTest(R1, R2, chi) = p-value of the White test for the X values in R1 and Y values in R2; if chi = TRUE (default) then the chi-square test is used; otherwise the F test is used.
The values in Figure 2 can be achieved by placing the formulas
=WhiteStat(C4:E53,B4:B53) in cell T5
=WhiteTest(C4:E53,B4:B53) in cell T7
=WhiteStat(C4:E53,B4:B53,FALSE) in cell T9
=WhiteTest(C4:E53,B4:B53,FALSE) in cell T12