Linear Combination of Coefficients

Objective

We show how to restrict the regression coefficients so that a linear combination of these coefficients is equal to some constant. In particular, suppose that the regression model is

Linear regression equation

and we constrain the coefficients by

Coefficient constraints

for some constants aj and c.

We now present two approaches for determining the regression coefficients subject to the above constraints.

Approach when a0 ≠ 0

In this case

b_0 formula, a_0 not zero

For all j > 0, let cj = –aj/a0 and let c0 = c/a0. It now follows that

Reformatted linear regression equation

If we use the data

Reformatted data values

we get the following regression model through the origin

Equivalent model through origin

The coefficients of this regression model can serve as the coefficients of the original model where in addition

b_0 formula

Approach when a0 = 0

We can assume that ak ≠ 0 for some k > 0. To make the notation easier, and without any loss of generality, let’s suppose that k = 1. In this case, we have

b_1 formula

For all j > 1, let cj = –aj/a1 and let c0 = c/a1. It now follows that

Regression model revised

If we use the data

Revised data

we obtain the regression model with n-1 coefficients

Revised regression model

The coefficients of this regression model can serve as the coefficients of the original model where in addition

b_1 formula

Example with a0 ≠ 0

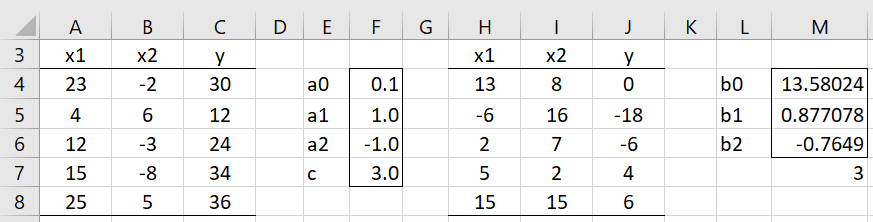
Example 1: Find the regression coefficients for the data in Figure 1 of Bounded Regression Coefficients (repeated in Figure 1 below) subject to the constraint .1b0 + b1 – b2 = 3.

The analysis is shown in Figure 1. First, we convert the data in range A3:C8 based on the aj values and the c value shown in column F to obtain the data shown in range H3:J8. E.g. the formula in cell H4 is =A4-$F$5/$F$4, the formula in cell I4 is =B4-$F$6/$F$4 and the formula in cell J4 is =C4-$F$7/$F$4.

We next find the coefficients for the data shown in range H3:J8 using regression through the origin (no intercept term). These are shown in range M5:M6 using the array formula =RegCoeff(H4:I8,J4:J8,FALSE). These are the x1 and x2 coefficients for the original regression subject to the constraints. The intercept coefficient for the original regression (shown in cell M4) is now calculated by the formula =(F7-SUMPRODUCT(F5:F6,M5:M6))/F4.

Constrained regression

Figure 1 – Constrained regression, a0 ≠ 0

Example with a0 = 0

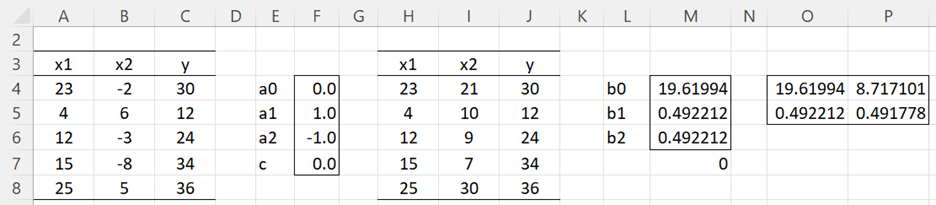
Example 2: Repeat Example 1 subject to the constraint b1 = b2.

This constraint is equivalent to b1 – b2 = 0. Note that this time a0 = 0, and so we use the second approach described above.

The analysis is shown in Figure 2. First, we convert the data in range A3:C8 based on the aj values and the c value shown in column F to obtain the data shown in range H3:J8. E.g. the formula in cell H4 is =$F$5*A4/$F$5, the formula in cell I4 is =B4+H4 and the formula in cell J4 is =C4-$F$7/$F$5. The remaining elements in columns H, I, and J are obtained by highlighting the range H4:J8 and pressing Ctrl-D.

We next find the coefficients for the data shown in range I3:J8 using linear regression. These are shown in range O4:P5 using the array formula =RegCoeff(I4:I8,J4:J8). The values in column O provide the intercept and x2 coefficients for the original regression subject to the constraints. The b1 coefficient for the original regression (shown in cell M5) is now calculated by the formula =F7/F5-SUMPRODUCT(F6:F6,M6:M6:M6)/F5.

Constrained regression a_0=0

Figure 2 – Constrained regression, a0 = 0

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack provides the following array function.

CRegCoeff(Rx, Ry, Rc): returns an n+1 × 1 column array with the regression coefficients for linear regression with X values in the m × n array Rx and Y values in the m × 1 column array Ry, based on the weights for the coefficients in the n+2 × 1 column array Rc.

The first entry in Rc is the multiplier of the intercept and the last entry in Rc is the constant. E.g. for the linear regression y = b0 + b1*x1 + b2*x2 subject to the constraint 2b0 – 3b2 = 4, we use the column array which is the transpose of (2, 0, -3, 4).

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Fruehwirth-Schnatter, S. (2012) Linear combination of parameters
https://statmath.wu.ac.at/~fruehwirth/Oekonometrie_I/Folien_Econometrics_I_teil5.pdf

Jun, J. (2021) Regression and linear combinations
https://jeremykun.com/2021/03/29/regression-and-linear-combinations/

Leave a Comment