Cochrane-Orcutt regression is an iterative version of the FGLS method for addressing autocorrelation. This approach uses the following steps for estimating rho.
Step 1: Run OLS regression on
and find the residuals e1, e2, …, en
Step 2: Using these sample residuals ei, find an estimate for ρ using OLS regression on εi = ρεi-1 + δi.
Step 3: Substitute this estimate for ρ in the generalized difference equation
Step 4: Based on step 3, new residuals can be calculated. Go to Step 2.
Continue this iteration until the change in the estimated value of ρ is less than some predetermined amount. Note that an iterative approach is used since regression coefficient r in step 2 is not necessarily an unbiased estimate of ρ, although it is known to be a consistent estimate of ρ (namely it will converge to ρ).
Example 1: Repeat Example 1 of FGLS Method for Autocorrelation using the Cochrane-Orcutt method.
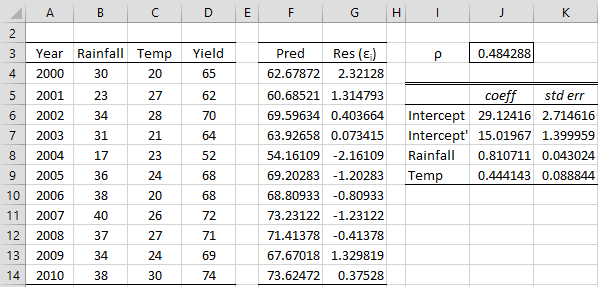
Figure 1 – Cochrane-Orcutt method (iteration 1)
The residuals from step 1 are shown in column G of Figure 1. The value of ρ in step 2 is shown in cell J3, as calculated by the array formula =RegCoeff(G4:G13,G5:G14,FALSE). We now calculate the regression coefficients (step 3) as shown in range J7:K9 using the array formula
=RegCoeff(B5:C14-J3*B4:C13,D5:D14-J3*D4:D13)
The intercept coefficient is corrected in cell J6 using the formula =J7/(1-J3), completing iteration # 1.
We now use these regression coefficients to calculate new values for the residuals, as displayed in Figure 2.
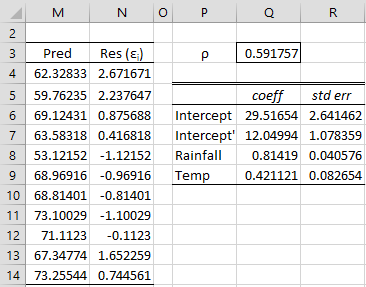
Figure 2 – Cochrane-Orcutt method (iteration 2)
Range M4:M14 (the predicted values) in Figure 2 contains the array formula =MMULT(B4:C14,J8:J9)+J6. The new residuals in range N4:N14 are calculated by the array formula =D4:D14-M4:M14.
The new rho value and regression coefficients are calculated as in Figure 2. Cell Q3 contains the formula =RegCoeff(N4:N13,N5:N14,FALSE), range P7:R9 contains the array formula =RegCoeff(B5:C14-Q3*B4:C13,D5:D14-Q3*D4:D13) and cell Q6 contains the formula =Q7/(1-Q3).
We can continue in this manner until there is convergence in calculating the rho value. This is the approach used by the following Real Statistics functions.
Real Statistics Functions: The following functions are available in the Real Statistics Resource Pack, where R1 contains the x data values and R2 contains the y data values.
CO_RHO(R1, R2, iter, prec) = the value of rho calculated using the Cochrane-Orcutt method based on iter (default 1000) iterations unless the change in the rho value is less than prec (default .0001), at which point the process stops.
COCoeff(R1, R2, rho): an array function which produces a k+1 × 2 array where column 1 contains the regression coefficients based on the rho and column 2 contains the corresponding standard errors. If rho is omitted then rho defaults to 1 – d/2 where d = the Durbin-Watson statistic.
CO_Coeff(R1, R2, iter, prec) = COCoeff(R1, R2, CO_RHO(R1, R2, iter, prec))
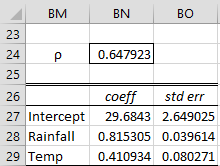
For Example 1, =CO_RHO(B4;C14, D4:D14) outputs the rho value of .647923. The output from the array formula =CO_Coeff(B4;C14, D4:D14) is shown in range BN27:BO29 of Figure 3. The formula =COCoeff(B4;C14, D4:D14, BN24) produces the same output.
Figure 3 – Cochrane-Orcutt functions
Hi Charles,
Im using the CO regression tool for time series data at country level. I’d like to include country and year dummy variables in my model.
If the transformation includes the dummy variables the transformed values for the 1’s are most often a decimal (i.e. non-1).
Is it feasible to transform only the country data (excluding the dummy variables) and thereafter add dummy variables for estimation via OLS?
Thank you,
Gareth
Hello Gareth,
I haven’t run into this situation before, but is there any reason why you could treat the dummy variables just like any of the other independent variables?
See the following for further information
https://forums.eviews.com/viewtopic.php?t=392
Charles
Thank you Charles.