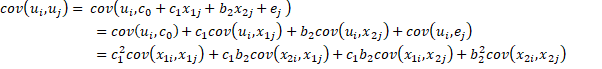Autocorrelation Introduction

Basic Concepts

When performing multiple linear regression using the data in a sample of size n, we have n error terms, called residuals, defined by e_i = y_i – ŷ_i. One of the assumptions of linear regression is that there is no autocorrelation between the residuals, i.e. for all i ≠ j, cov(e_i, e_j) = 0.

Definition 1: The autocorrelation (aka serial correlation) between the data is cov(e_i, e_j). We say that the data is autocorrelated (or there exists autocorrelation) if cov(e_i, e_j) ≠ 0 for some i ≠ j.

First-order autocorrelation occurs when consecutive residuals are correlated. In general, p-order autocorrelation occurs when residuals p units apart are correlated.

Observation: Since another assumption for linear regression is that the mean of the residuals is 0, it follows that

cov(e_i, e_j) = E[(e_i–0)(e_j–0)] = E[e_ie_j]

and so data is autocorrelated if E[e_ie_j] for some i ≠ j.

Example 1: Find the first-order autocorrelation for the regression of rainfall and temperature on crop yield for the data in range A3:D14 of Figure 1.

Figure 1 – First-order autocorrelation

The predicted Yield values are shown in column F and the Residuals are shown in column G. The predicted values in range F4:F14 are calculated by the array formula =TREND(D4:D14,B4:C14) and the residuals in range G4:G14 are calculated by the array formula =D4:D14-F4:F14. The first-order autocorrelation is .58987 (cell G16) as calculated by the formula =CORREL(G4:G13,G5:G14).

Sources of Autocorrelation

We now give some of the reasons for the existence of autocorrelation.

In the case of stock market prices, there are psychological reasons why prices might continue to rise day after day until some unexpected event occurs. Then after some bad news, prices may continue to fall. Thus, it is common for time series data to exhibit autocorrelation.

Sometimes an event takes time to have an effect. Prices for oil may rise due to under-supply or increased demand, which results in increased production, which has a delayed effect in price reductions, which in turn may result in decreased production, etc. Oil price data, in this case, will show p-order autocorrelation where p is the lag time for this effect.

Autocorrelation may also be caused by an incorrectly specified regression model. E.g. suppose the true regression model is

using two independent variables x₁ and x₂. Thus, b₂ ≠ 0 and, based on the usual regression assumptions, cov(x_i, e_j) = 0 and cov(e_i, e_j) = 0. Also, for any random variable u and constant c, cov(u, c) = 0.

But now suppose that you use a model instead which leaves out the x₂ variable, say

The residual term u_i in the deficient model can be expressed as u_i = c₀ + c₁x_1i + b₂x_2i + e_i where c₀ = b₀ – a₀ and c₁ = b₁ – a₁. It follows that

Thus

Since it is quite likely that there is correlation between the data elements, it is quite likely that cov(u_i, u_j) ≠ 0, i.e. there is autocorrelation.