Finding multinomial logistic regression coefficients using Newton’s method

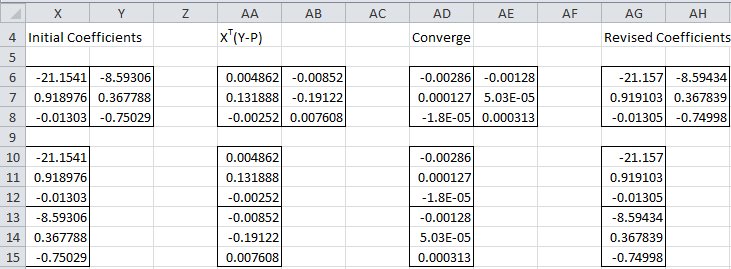
Instead of using Solver, we can use Property 3 of Basic Concepts of Multinomial Logistic Regression to calculate the multinomial logistic regression coefficients. In order to demonstrate how to use Newton’s method, we initialize the coefficients with the result from Solver shown in Figure 2 of Finding Multinomial Logistic Regression Coefficients using Solver and perform one iteration using the equation in Property 3 of Basic Concepts of Multinomial Logistic Regression,

Figure 1 – One iteration of Newton’s Method

The key formulas used in Figure 1 are shown in Figure 2.

Figure 2 – Key formulas from Figure 1

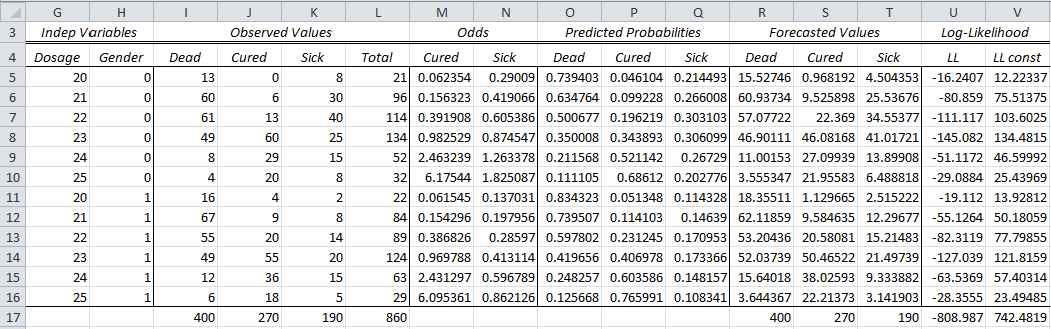
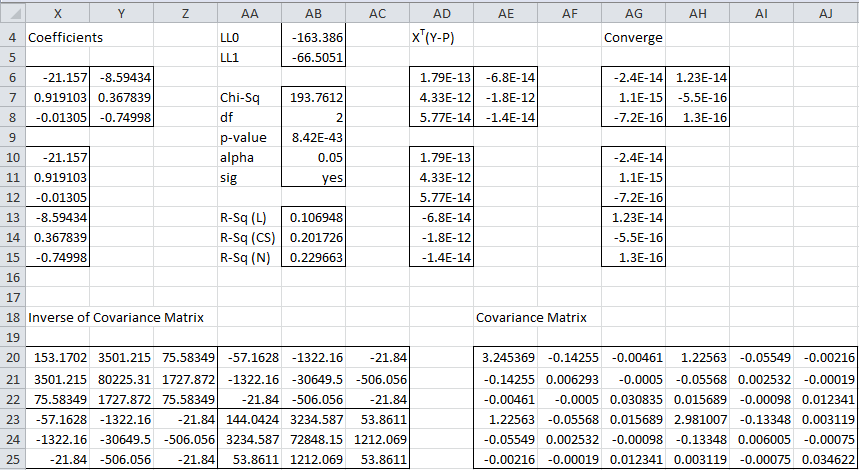
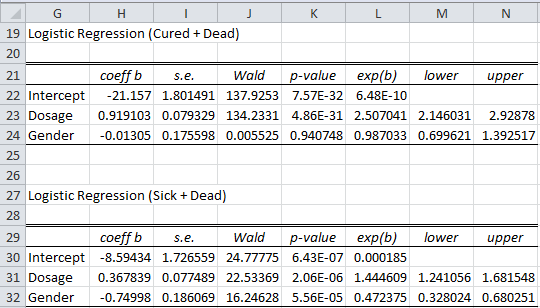
If we set the initial values of coefficients to zeros then we can use Newton’s Method to find the values of the multinomial logistic regression coefficients (e.g. using the MLogitCoeff supplemental function described in Finding Multinomial Logistic Regression Coefficients) as shown in the following figures.

Figure 3 – Multinomial logistic reg. via Newton’s Method (part 1)

Figure 4 – Multinomial logistic reg. via Newton’s Method (part 2)

Figure 5 – Multinomial logistic reg. via Newton’s Method (part 3)