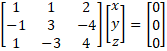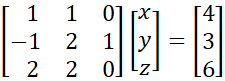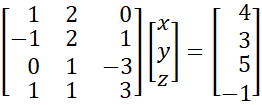Representation of systems of linear equations
Definition 1: A set of n linear equations
in k unknowns xj can be viewed as the matrix equation AX = C where A is the n × k matrix [aij], X is the k × 1 column vector [xj] and C is the n × 1 column vector [cj].
Property 1: If A is a square matrix (i.e. the number of equations is equal to the number of unknowns), the equation AX = C has a unique solution if and only if A is invertible (i.e. det A ≠ 0), and in this case, the unique solution is given by X = A–1C.
Proof: Suppose A is invertible. It now follows that X = A–1C is a solution to AX = C since AX = A(A–1C) = (AA–1)C = IC = C.
Suppose AX = C. Then A–1C = A–1(AX) = (AA–1)X = IX = X, and so this solution is unique.
The converse is a consequence of Property 4 of Rank of a Matrix.
Cramer’s Rule
Property 2 (Cramer’s Rule): If the square matrix A is invertible, the unique solution to AX = C is given by
where Aj is A with the jth column replaced by the entries of C.
Example 1: Solve the following linear system using Cramer’s Rule:
In Figure 2, we calculate det A and det Aj for each j.

Figure 1 – Calculating a determinant using Cramer’s rule
It now follows that x = -6/9 = -2/3, y = 3/9 = 1/3 and z = 0/9 = 0.
Per Property 1, we can get the same result by calculating A–1 C, which can be carried out in Excel using the formula =MMULT(MINVERSE(A), C). For Example 1, this yields
Definition 2: When C from Definition 1 is not the null matrix, then the linear equations are called heterogeneous. When C = Ο the linear equations are called homogeneous. In this case, Ο is a solution of AX = Ο, called the trivial solution.
Property 3: If A is invertible then X = Ο is the only solution of AX = Ο.
Proof: This follows from Property 1.
Observation: When A is not invertible (i.e. det A = 0) any scalar multiple of a non-trivial solution to the homogeneous equation AX = Ο is also a solution. To find such a solution we can use the Gaussian Elimination method, a method which is similar to the one we used to calculate the determinant of a square matrix based on Property 5 of Determinants and Linear Equations. This approach works for any A (whether square or not, and whether invertible or not).
Gaussian Elimination
Definition 3: If A is an n × k matrix and B is an n × m matrix then the augmented matrix A|B is an n × (k+m) matrix whose first k columns are identical to the columns in A and whose remaining m columns are identical to the columns in B.
Property 4: If A′ and C′ are derived from A and C based on any one of the following transformations, then the equations AX = C and A′X = C′ have the same solutions.
- Interchange of any two rows
- Multiplication of any row by a constant
- Addition of any row multiplied by a constant to another row
Observation: Typically we apply the above transformations to the augmented matrix A|C.
Definition 4: The Gaussian Elimination Method is a way of solving linear equations and is based on the transformations described in Property 9. Suppose A and C are as described in Definition 1.
Step 0 – set i = 1 and j = 1
We now apply the following series of transformations to the augmented matrix (step 1 through step p where p is the smaller of n and k):
Step i – part 1: Find r ≥ i such that the absolute value of arj is largest. If arj ≈ 0 (i.e. |arj| < ϵ where ϵ is some predefined small value), then if j = n terminate the procedure; otherwise replace j by j + 1 and repeat step i. If not arj ≈ 0 and r > k then exchange rows r and i (rule 1).
Step i – part 2: Divide all the entries in row i by aij (rule 2).
Step i – part 3: For every row r below row i, add –arj times row i to row r (rule 3). This guarantees that arc = 0 for all r > i and c ≤ j.
Observation: For non-homogeneous equations (i.e. C ≠ Ο) there are three possibilities: there are an infinite number of solutions, there are no solutions or there is a unique solution. For homogeneous equations (i.e. C = Ο) there are two possibilities: there are an infinite number of solutions or there is a unique solution, namely the trivial solution where X = Ο.
Gaussian Elimination Examples
Example 2: Solve the following linear system using Gaussian Elimination:
Figure 2 displays the steps in the Gaussian Elimination process for Example 2.
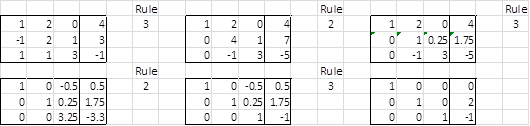
Figure 2 – Solving linear equations using Gaussian elimination
Since A transforms into the identity matrix, we know that the transform of C is the unique solution to the system of linear equations, namely x = 0, y = 2, and z = -1. Note that we get the same result by calculating X = A–1 C.
Example 3: Solve the following homogeneous linear system using Gaussian Elimination:
By Gaussian Elimination from Figure 3 we see that the only solution is the trivial solution:
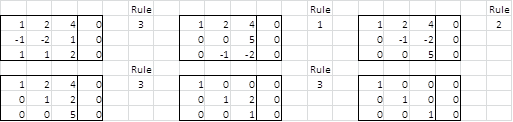
Figure 3 – Solving a homogeneous linear equation
Example 4: Solve the following homogeneous linear system using Gaussian Elimination:
This time Gaussian Elimination produces a row with all zeros (see Figure 4), and the number of non-zero rows = 2 < 3 unknowns. Thus there is an infinite number of solutions.
Figure 4 – Finding solutions to homogeneous linear equations
The solutions can take the form x = -2.5t, y = .5t, z = t for any value of t.
Observations
As we can see from the above examples, a homogeneous equation AX = O, where A is an m × n matrix, has a unique solution when there are n non-zero rows after performing Gaussian Elimination. Otherwise, the equation has an infinite number of solutions.
As we saw in Example 4, sometimes there is an infinite number of solutions to a system of linear equations, each of which is expressed as a multiple of one solution. In general, when there are multiple solutions, each solution can be expressed as a linear combination of column vectors as described in more detail in Multiple Solutions to Linear Equations.
Matrix Inversion
Gaussian Elimination can also be used to invert a square n × n matrix A by applying the above procedure to A|In. If the procedure terminates before n steps have been completed then A is not invertible. If the procedure terminates after n steps (in which case A′ = In) then C′ = A–1.
Example 5: Use Gaussian Elimination to invert the matrix
The result is shown in Figure 5.

Figure 5 – Inverting a matrix using Gaussian elimination
The fact that A transforms into the identity matrix indicates that A is invertible. The inverse is given by the transformation of the identity matrix, namely
This is the same result as using the Excel formula MINVERSE(A).
Worksheet Functions
Real Statistics Functions: The following array functions are provided for carrying out the Gaussian Elimination procedure.
ELIM(R1, prec): an array function that outputs the results of Gaussian Elimination on the augmented matrix found in the array R1. The shape of the output is the same as the shape of R1.
LINEQU(R1, prec): an array function that returns an n × 1 column vector with the unique solution to equations defined by the augmented m × (n+1) matrix found in array R1; returns a vector consisting of #N/A! if there is no solution and a vector consisting of #NUM! if there are an infinite number of solutions.
By default, each of these functions assumes that an entry with an absolute value less than 0.0001 is equivalent to zero. This is necessary since small values are not treated as zero in the Gaussian elimination algorithm described above. You can change this default value to something else by inserting a second parameter in either of these functions: e.g. ELIM(R1, prec) or LINEQU(R1, prec). Thus ELIM(R1) = ELIM(R1, 0.0001).
Data Analysis Tool
Real Statistics Data Analysis Tool: The Solve Set of Linear Equations data analysis tool contained in the Real Statistics Resource Pack provides equivalent functionality to LINEQU and ELIM. To use this tool, enter Ctrl-m and select Solve Set of Linear Equations from the menu. When a dialog box appears, fill in the Input Range (with the same range as R1 above). Selecting Show solution only is equivalent to LINEQU(R1), while not clicking on this option is equivalent to ELIM(R1).
LINEQU and ELIM Examples
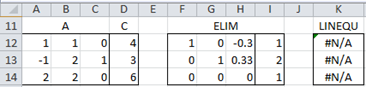
Example 6: Solve the following linear system using the appropriate Real Statistics functions.
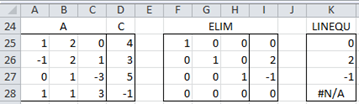
Figure 6 shows matrix A, in range A12:C14, vector C in range D12:D14. The array function =ELIM(A12:D14) in range F12:I14 applies Gaussian Elimination. Since the last row has zeros in the columns corresponding to A and 1 in the last column (i.e. 0 = 1), we conclude there is no solution. This is corroborated using the array function =LINEQU(A12:D14) in range K12:K14 since the results are all #N/A.
Figure 6 – Finding solutions using ELIM and LINEQU
Example 7: Solve the following linear system using the appropriate Real Statistics functions.
For all the examples we have given so far, the number of equations is equal to the number of unknowns (i.e. A is a square matrix). In this example, we have 4 equations in 3 unknowns, yet there is a unique solution. After applying Gaussian elimination, we see in Figure 7 that the last row (range F28:I28) consists of all zeros, and so we have the equivalent of a 3 equations in 3 unknowns. The unique solution for this example is x = 0, y = 2, z = -1.
Figure 7 – Finding solutions where A is not square
More Observations
As we can see from the above examples, a non-homogeneous equation AX = C, where A is an m × n matrix and C is a m × 1 vector, has no solution when after applying Gaussian elimination some row has all zero except in the last column where there is a non-zero entry. When this is not the case, AX = C has a unique solution when there are n non-zero rows and it has an infinite number of solutions otherwise.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2020) System of linear equations
https://en.wikipedia.org/wiki/System_of_linear_equations
Golub, G. H., Van Loan, C. F. (1996) Matrix computations. 3rd ed. Johns Hopkins University Press
Searle, S. R. (1982) Matrix algebra useful for statistics. Wiley
Perry, W. L. (1988) Elementary linear algebra. McGraw-Hill
Fasshauer, G. (2015) Linear algebra.
https://math.iit.edu/~fass/532_handouts.html
Lambers, J. (2010) Numerical linear algebra
https://www.yumpu.com/en/document/view/41276350