Newton’s Method

Basic Concepts

Newton’s Method is traditionally used to find the roots of a non-linear equation.

Definition 1 (Newton’s Method): Let f(x) = 0 be an equation. Define x_n recursively as follows:

Here f′(x_n) refers to the derivative f(x) of at x_n.

Property 1: Let x_n be defined from f(x) as in Definition 1. As long as function f is well-behaved and the initial guess is suitable, then f(x_n) ≈ 0 for sufficiently large n.

Newton’s method requires that f(x) has a derivative and that the derivative not be zero. Usually, the method converges quickly to a solution, but this can depend on the initial guess. Also in cases where there are multiple solutions, different initial guesses can lead to different solutions.

Click here for a description of the Real Statistics worksheet function NEWTON that implements Newton’s method.

Example (one unknown)

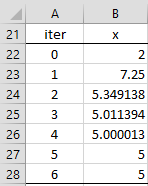
Example 1: Use Newton’s Method to find the square root of 25.

The problem is equivalent to solving the equation f(x) = 0 where f(x) = x² – 25.

From calculus, f′(x) = 2x, and so

Suppose we start the iteration with x₀ = 2, then as we see in Figure 1, the iterations converge to 5 as expected.

Figure 1 – Newton’s Method for Example 1

Note that if we select x₀ = 0 the algorithm won’t converge to a solution since f(x) would be undefined. Also if we set x₀ = -2 (or any negative value) then the procedure iterates to -5, which is the other solution to f(x) = 0.

Multivariate Version

We now extend Newton’s method to m equations in m unknowns.

Definition 2 (Newton’s Method): Let X = [x_i] be an m × 1 column vector and let F = [f_i] be an m × 1 column vector of functions. Our objective is to solve the set of m equations given by F(x) = Ο (here Ο is the zero vector).

Let J = [q_ij] be the Jacobian matrix, defined by the partial derivatives q_ij = . Now define the m × 1 column vectors X_n and the m × m matrices J_n as follows

Property 2: Using the terminology in Definition 2, then for a well-behaved F, a reasonable guess and sufficiently large n, F(X_n) ≈ Ο.

Click here for a description of the Real Statistics worksheet functions NEWTON2 and NEWTON3 that implement Newton’s method for two or three variables.

Example (two unknowns)

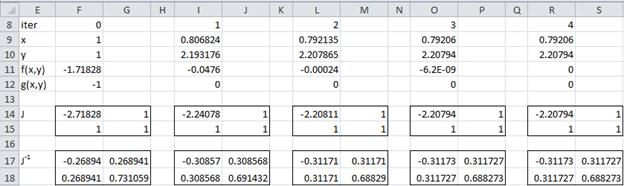
Example 2: Find the solution to the equations y – e^x = 0 and x + y = 3.

Set f(x, y) = y – e^x and g(x, y) = x + y – 3. Then we need to find the solution to f(x, y) = 0  and  g(x, y) = 0 , i.e.  F(X) = Ο where X =   and F = . Now

where we use the notation f_x(x,y) to mean . Starting with X₀ = , we see in Figure 2 that the procedure converges to x = 0.79206 and y = 2.20794 after 3 iterations.

Figure 2 – Newton’s Method for Example 2

Representative formulas for the worksheet in Figure 2 (for iteration 2) are shown in Figure 3.

Figure 3 – Formulas for 2^nd iteration

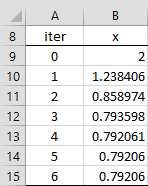
The example was chosen so that we could check the result using Newton’s method in one variable since the problem is equivalent to e^x + x – 3 = 0 and y = 3 – x. We can therefore apply Newton’s method as in Example 1, with f(x) = e^x + x – 3, f′(x) = e^x + 1, and so

The iteration proceeds as in Figure 4.

Figure 4 – Alternative use of Newton’s Method for Example 2

Thus x = 0.79206 and y = 3  – x = 3 – 0.79206 = 2.20794, as before.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2012) Newton’s method
https://en.wikipedia.org/wiki/Newton%27s_method

Wiersma, A. (2016) The complex dynamics of Newton’s method
https://fse.studenttheses.ub.rug.nl/14180/1/Alida_Wiersma_2016_WB.pdf