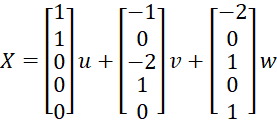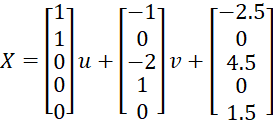Objective
In Example 4 of System of Linear Equations, we found that there was an infinite number of solutions to a system of linear equations. Each solution could be expressed as a multiple of one solution. In general, when there are multiple solutions, each solution can be expressed as a linear combination of column vectors. We explore this in more detail on this webpage.
Examples
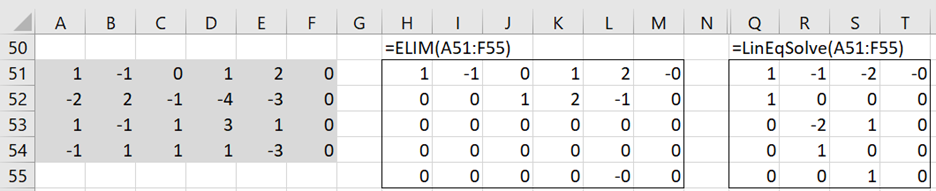
Example 1: Range A51:F54 of Figure 1 shows a system of 4 homogeneous linear equations in 5 unknowns. The reduced form after applying Gaussian elimination is shown in the middle of the figure.
Figure 1 – System of homogeneous linear equations
Looking down the main diagonal of the reduced form, we observe there are 1’s for the x1, x3 variables, and so x2, x4 and x5 are the free variables, i.e. they can take any values. Thus, we can set these variables to the parameters u, v and w as follows: x2 = u, x4 = v, x5 = w. Thus,
This is equivalent to the solutions
Any solution takes the form of a linear combination of three column vectors.
Observation: The situation is similar for non-homogeneous equations. In this case, when there are multiple solutions, each solution can be expressed as a linear combination of column vectors plus one constant column vector.
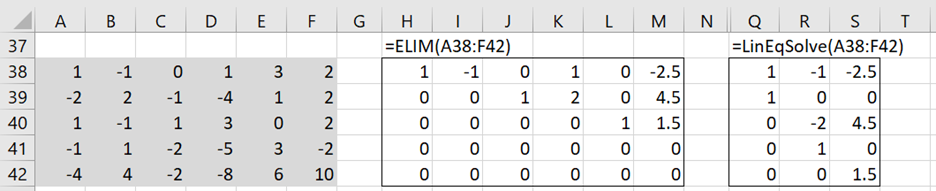
Example 2: Range A38:F42 of Figure 2 shows a system of 5 non-homogeneous linear equations in 5 unknowns. The reduced form after applying Gaussian elimination is shown in the middle of the figure.
Figure 2 – System of non-homogeneous linear equations
Looking down the main diagonal of the reduced matrix, we see that there are 1’s for the x1, x3 and x5 variables, and so x2 and x4 are the free variables, i.e. they can take any values. Setting these variables to the parameters u and v we obtain the equations
This is equivalent to the solutions
Any solution takes the form of a linear combination of the first two column vectors plus the third column vector.
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack provides the following array function which automates the above process.
LinEqSolve(R1, prec): an array function that outputs the solution matrix for the system of linear equations defined by the augmented matrix found in the array R1. The number of rows in the output is one less than the number of columns in R1.
During Gaussian elimination, values less than prec (default .0001) are treated as zero.
If the system of linear equations does not have a solution, then the error value #N/A is returned. If there is a unique solution (including the trivial solution for a system of homogeneous equations), then the output will consist of a column array with this solution.
We can use the LinEqSolve function to find all the solutions for Example 1 as shown on the right side of Figure 1. Similarly, all the solutions for Example 2 are shown on the right side of Figure 2.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2020) System of linear equations
https://en.wikipedia.org/wiki/System_of_linear_equations