Real Statistics Data Analysis Tool: The Real Statistics Resource Pack provides the Matrix Operations data analysis tool, which supports a number of matrix operations. These work just like the corresponding worksheet array functions TRANSPOSE, MINVERSE, etc. (see, for example, Matrix Operations), except that you don’t need to specify the shape and size of the matrix since these are determined automatically from the shape and size of the input matrix.
Example
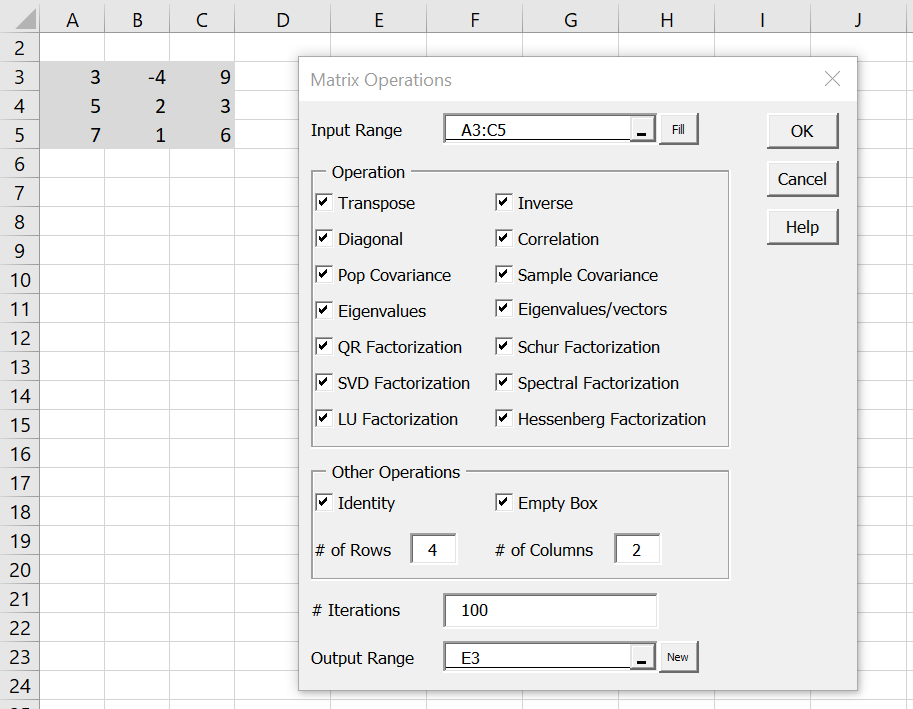
Example 1: Perform all the operations supported by the Matrix Operations data analysis tool for the matrix in range A3:C5 of Figure 1.
After pressing Ctrl-m and selecting the Matrix Operations option (from the Desc tab if using the MultiPage user interface), a dialog box appears as shown on the right side of Figure 1. Next, click on all the options as shown in the figure.
Figure 1 – Data and dialog box
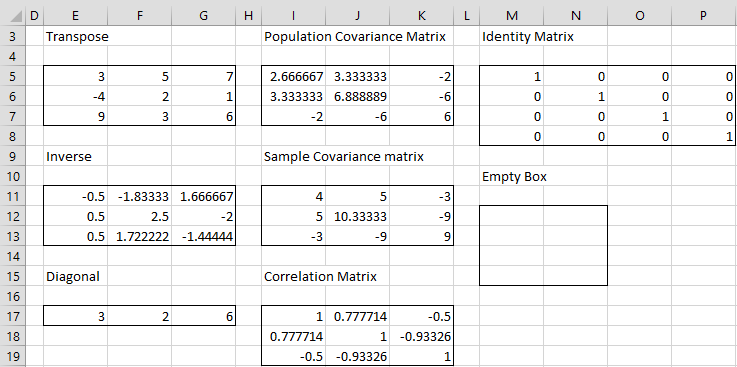
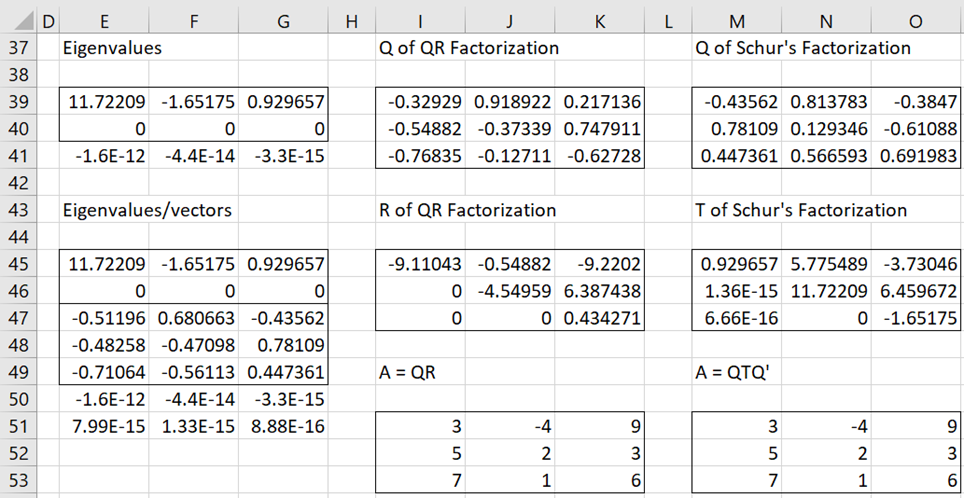
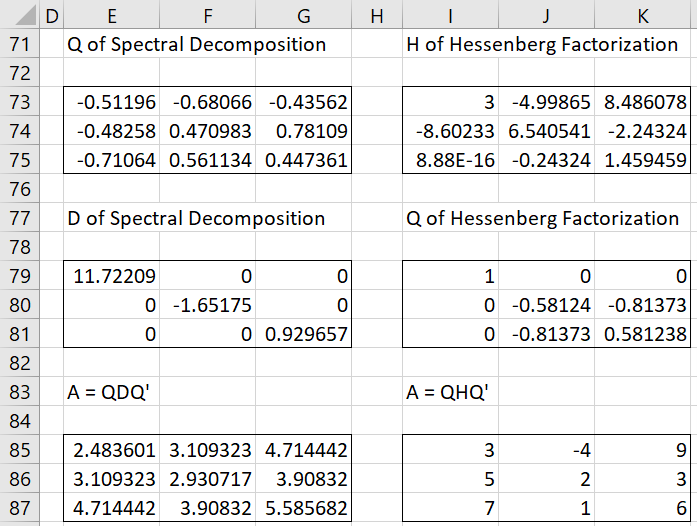
After clicking on the OK button, the results shown in Figures 2, 3, 4, and 5 appear (slightly reformatted).
Output
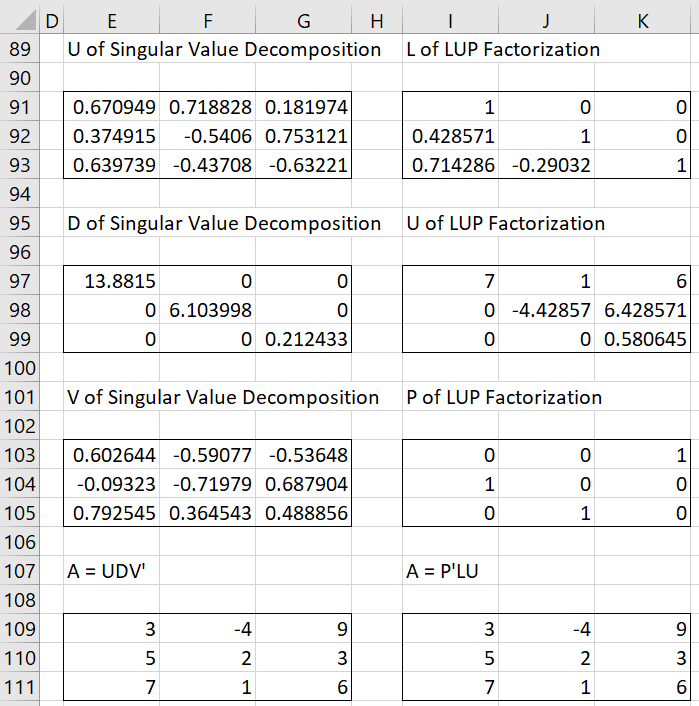
Figure 2 – Output from Matrix data analysis tool (part 1)
Figure 3 – Output from Matrix data analysis tool (part 2)
Figure 4 – Output from Matrix data analysis tool (part 3)
Figure 5 – Output from Matrix data analysis tool (part 4)
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Cliff Notes (2021) Operations with matrices
https://www.cliffsnotes.com/study-guides/algebra/linear-algebra/matrix-algebra/operations-with-matrices
Better Solutions (2021) Matrix functions
https://bettersolutions.com/excel/functions/matrix-category.htm