Matrix Operations

Matrix Addition and Subtraction

Definition 1. You can add and subtract matrices of the same shape.

Let A and B be r × c matrices with A = [a_ij] and B = [b_ij]. Then A + B is an r × c matrix with A + B = [a_ij + b_ij] and A – B is an r × c matrix with A – B = [a_ij – b_ij].

Operations between a Matrix and a Scalar

Definition 2: A matrix can be multiplied (or divided) by a scalar. A scalar can also be added to (or subtracted from) a matrix.

Let A be an r × c matrix with A = [a_ij] and let b be a scalar. Then bA and A + b are r × c matrices where bA = [b · a_ij] and A + b = [a_ij + b]. We can define Ab and b + A in a similar fashion. Clearly, b + A = A + b and Ab = bA. Division and subtraction of matrices by scalars can be defined similarly.

Matrix Multiplication

Definition 3: You can multiply two matrices, but only if they have compatible shapes.

Let A be a p × m matrix with A = [a_ij], and let B be an m × n matrix with B = [b_jk]. Then AB is a p × n matrix with AB = [c_ik] where

Observation: For the multiplication AB to be valid, the number of columns in A must equal the number of rows in B. The resulting matrix will have the same number of rows as A and the same number of columns as B.

The associative law holds, namely (AB)C = A(BC), i.e. it doesn’t matter whether you multiply A by B and then multiply the result by C or first multiply B by C and then multiply A by the result. It is essential that the matrices have a compatible shape. Thus if A is p × m, B is m × n and C is n × s then ABC will have the shape p × s. The distributive laws, namely A(B + C) = AB + BC and (A + B)C = AC + BC, also hold.

The commutative law of addition holds, namely A + B = B + A, but the commutative law of multiplication does not hold even when the matrices have a suitable shape; thus, even for two n x n matrices A and B, AB is not necessarily equal to BA. For square matrices, the trace of AB is equal to the trace of BA though.

Trace and Matrix Operations

Property 0: For square matrices A and B of the same size and shape and scalar c:

1. Trace(A+B) = Trace(B+A)
2. Trace(cA) = c Trace(A)
3. Trace(AB) = Trace(BA)

Proof: The proofs are straightforward, based on the definition of trace and matrix addition and multiplication.

Transpose of a Matrix

Definition 4: The transpose of an r × c matrix A = [a_ij]   is the c  × r matrix A^T = [a_ji].

A (square) matrix A is symmetric if A = A^T

Property 1:

1. (A^T)^T = A
2. (AB)^T = B^TA^T
3. If A and B are symmetric and AB = BA then AB is symmetric
4. Trace(A) = Trace(A^T)

Proof: We prove (c). Assume that A and B are symmetric. By Definition 4 and Property 1b, AB = A^TB^T = (BA)^T = (AB)^T

Observation: If A is a column vector then A^TA is a scalar. In fact, A^TA = ‖A‖². Thus, a column vector A is a unit vector if and only if A^TA = 1.

Inverse of a Matrix

Definition 5: An n × n matrix A is invertible (also called non-singular) if there is a matrix B such that AB = BA = I_n (where I_n is the n × n identity matrix). A^–1 is the inverse of A provided AA^–1 = A^–1A = I_n. A matrix that is not invertible is called singular.

Property 2: If A is invertible, then its inverse is unique.

Proof: Suppose B and C are inverses of A. Then by the associative law,  C = IC = (BA)C = B(AC) = BI = B, and so C = B.

Observation: In fact, if there is a matrix B such that AB = I_n or BA = I_n then A is invertible and A^–1 = B.

Property 3:  If A and B are invertible, then (A^–1)^–1 = A and (AB)^–1 = B^–1 A^–1

Proof: The first assertion results from the first assertion of Property 2.

Since (AB)(B^–1A^–1) = A(BB^-1)A^–1,= AIA^–1 = AA^–1 = I the second assertion follows from the second assertion of Property 2.

Property 4: If A is invertible, then so is its transpose and (A^T)^-1 = (A^-1)^T

Proof: By Property 1b, A^T(A^-1)^T = (A^-1A)^T = I^T = I. Similarly, (A^-1)^TA^T = (AA^-1)^T = I^T = I.

Property 5: A is symmetric if and only if A^-1 is also symmetric

Proof: Assume A is symmetric, then by Property 4,  (A^-1)^T = (A^T)^-1 = A^-1, and so A^-1 is also symmetric. For the converse, assume that A^-1 is symmetric, then from the above, it follows that (A^-1)^-1 is symmetric, but by Property 3, this means that A is symmetric.

Example 1: Find the inverse of

Since the inverse of A takes the form

where AA^–1 = I₂, it follows that

Thus we need to solve the following four linear equations in four unknowns:

Solving these equations yields a = 2/3, b = -1/3, c = 1/3, d = 1/3, and so it follows that

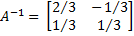Excel Functions

Excel Functions: Excel provides the following array functions to carry out the various matrix operations described above (where we conflate the matrices A and B with the arrays on an Excel worksheet that contain these arrays).

MMULT(A, B): If A is a p × m array and B is an m × n array, then MMULT(A, B) = the p × n matrix AB. 

MINVERSE(A): If A is an n × n square array, then MINVERSE(A) = A^–1. 

TRANSPOSE(A): If A is an m × n array, then TRANSPOSE(A) = A^T. 

Note that since these are array functions, most Excel users can’t simply press Enter when using these functions. E.g. for MMULT, you must first highlight a p × n  range before entering =MMULT(A,B) and then you must press Ctrl-Shft-Enter. This is not necessary for Excel 2021 and Excel 365 users where MMULT can be treated as a dynamic array function.

Versions of Excel starting with Excel 2013 also provide the array function MUNIT(n) which returns the n × n identity matrix.

You can also transpose an array A in Excel by copying the array (i.e. by highlighting the array and pressing Ctrl-C), clicking where you want A^T located (i.e. the cell at the upper left corner of A^T), and then selecting Home > Clipboard|Paste and choosing the Transpose option.

Using the +, -, *, /, and ^ operators with matrices

In addition, if A and B are defined as arrays (e.g. they are named arrays or entities such as B5:F8 or they are the results of matrix operations such as TRANSPOSE, INVERSE, or MMULT, then they can be manipulated using the +, -, *, / and ^ operators. These operations are done on a cell-by-cell basis.

For example, suppose range B2:C3 contains

If you highlight range D7:E8, enter =2*B2:C3+TRANSPOSE(B2:C3) and then press Ctrl-Shft-Enter, D7:E8 will contain

Note that D7:E8 must have the same shape as B2:C3 or an error will result. The following also holds.

Note too that if A is an m × n matrix and B is a 1 × n matrix (i.e. a row vector) then A + B is a valid operation in Excel and gives the same result as A + C where C is an m × n matrix all of whose rows contain the same data as B. Similarly you can calculate A – B, A*B and A/B. Also, you can calculate A + B, A – B, A*B, and A/B where B is an m × 1 column vector.

E.g. Suppose B2:C3 contains  and E2:E3 contains . If you highlight F4:G5, enter =B2:C3–E2:E3 and then press Crtl-Shft-Enter, F4:G5 will contain .

Matrix products, differences, and power

Real Statistics Functions: The Real Statistics Resource Pack supplies the following functions:

MPOWER(A,n) = Aⁿ

MSUB(A,B) = A – B

MPROD(A,B,C,D) = ABCD

Note that for MSUB, arrays A and B must have the same size and shape. Also, for any element in A and/or B that is not numeric, the corresponding element in the output will be blank.

MPROD can be used with 2, 3, or 4 compatible arrays. The function MPROD(A,B) is equivalent to MMULT(A,B). MPROD(A,B,C) is equivalent to MMULT(MMULT(A,B),C). MPROD(A,B,C,D) is equivalent to MMULT(MMULT(A,B),MMULT(C,D)).

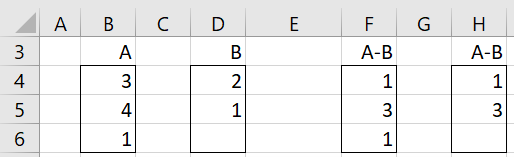
Example 2: Find A⁴ where A is the 2 × 2 matrix shown in range B4:C5 of Figure 2.

Figure 2 – MPOWER

The result is shown in range K4:L5. You can obtain the same result via the array formula =MMULT(H4:I5,B4:C5) or =MMULT(B4:C5,MMULT(B4:C5,MMULT(B4:C5,B4:C5))). Alternatively, you can use the array formula =MPOWER(B4:C5,4).

Example 3: Find A-B for the arrays shown in Figure 3.

Figure 3 – MSUB

Using the Excel array formula =B4:B6-D4:D6, we obtain the result shown in range F4:F6. Here the blank in cell D6 is treated as a zero. If cell D6 had contained any other non-numeric cell, then cell F6 would contain an error value. Using the Real Statistics formula =MSUB(B4:B6,D4,D6), we instead obtain the result shown in range H4:H6, where any non-numeric cell is treated as a blank.

Independence

Definition 6: Vectors X₁, …, X_k of the same size and shape are independent if for any scalar values b₁, … b_k, if b₁ X₁ +⋯+ b_k X_k = 0, then b₁ = … = b_k  = 0.

Vectors X₁, …, X_k are dependent if they are not independent, i.e. there are scalars b₁, … b_k, at least one of which is non-zero, such that b₁ X₁ +⋯+ b_k X_k = 0. 

Observation: If X₁, …, X_k are independent, then X_j ≠ 0 for all j.

Property 6: X₁, …, X_k are dependent if and only if at least one of the vectors can be expressed as a linear combination of the others.

Proof: Suppose X₁, …, X_k are dependent. Then there are scalars b₁, … b_k, at least one of which is non-zero such that b₁ X₁ +⋯+ b_k X_k = 0. Say b_i ≠ 0. Then

Now suppose that X_i = . Then b₁ X₁ +⋯ + b_k X_k = 0, where b_i = -1, and so X₁, …, X_k  are dependent.

Dot Product

Definition 7: The dot product of two vectors X = [x_i] and Y = [y_j] of the same shape is defined to be the scalar

If X and Y are n × 1 column vectors, then X∙Y = X^TY = Y^TX. Also ||X|| = √X·X.

Excel Function: If R1 is an array containing the data in X and R2 is an array containing the data in Y then the dot product X · Y = SUMPRODUCT(R1, R2).

Definition 8: Two non-null vectors of the same shape are orthogonal if their dot product is 0.

Real Statistics Tool

Click here for a description of Real Statistics’ Matrix Operations data analysis tool.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Cliff Notes (2021) Operations with matrices
https://www.cliffsnotes.com/study-guides/algebra/linear-algebra/matrix-algebra/operations-with-matrices

Better Solutions (2021) Matrix functions
https://bettersolutions.com/excel/functions/matrix-category.htm