Goal Seek
Excel provides a capability called goal-seeking which enables you to find the roots of a polynomial equation and a variety of other problems which are typically solved using iterative methods. Essentially you want to find a value of x such that f(x) = a for a constant a.
Excel’s goal-seeking capability can be found by going to the Data tab, pressing the small down arrow to the right of the What-If Analysis option, and then selecting Goal Seek. A small dialog box appears and you need to enter values for the following fields:
- Set cell
- To value
- By changing cell
Set cell should point to the cell that contains a formula for f(x). To value should contain the value a. By changing cell should point to a cell that has the initial guess of the value of x. When you press OK, Excel tries to find a value of x such that f(x) ≈ a. If the iteration converges then Excel will return the solution x in the cell where you put your initial guess.
For problems where there are multiple values of x such that f(x) = a, different initial guesses for x can yield different solutions. Thus, finding all the solutions requires repeated trials based on different guesses.
Starting with Excel 2016, there is no What-If Analysis option; instead, you use the Forecast option, and so the selection sequence is Data > Forecast|Goal Seek instead of Data > Data Tools|What-If Analysis > Goal Seek.
Examples
We can use Goal Seek, for example, to find the sample size required to achieve a specified power for various tests (see, for example, Power of a Sample or Power for t Distribution). We now show how to use Goal Seek to find the eigenvalues of a matrix.
Example 1: An eigenvalue of a matrix A is a constant c with the property that det(A–cI) = 0. Find the eigenvalues of the square matrix A in range A4:D7 of Figure 1.
We are seeking values c such that det(A–cI) = 0 (see Determinant of a Matrix). To accomplish this goal we have created the Excel worksheet described in Figure 1.
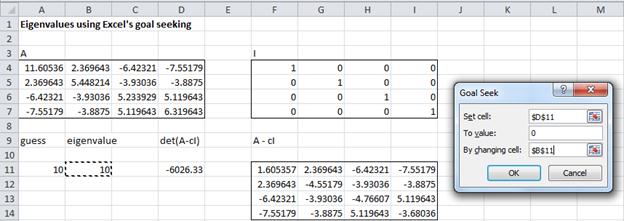
Figure 2 – Data for Example 1 plus Goal Seek dialog box
We have placed array A in range A4:D7 and the identity matrix with the same shape as A in range F4:I7. We now make an initial guess for the eigenvalue of 10 (cell B11). Since Excel will automatically change this value we also put the 10 in cell A11 so that we can recall the value of our initial guess. Next, we put the array formula for A–cI in the worksheet. In the above example, we highlight the array F11:I14 and type =A4:D7-B11*F4:I7, and then press Ctrl-Shft-Enter. Finally, we put the value det(A–cI) in the worksheet by entering =MDETERM(F11:I14) in cell D11.
Filling in the Goal Seek Dialog Box
We next access the Goal Seek dialog box as described above and enter the following values:
- Set cell: D11 – i.e. the formula for det(A–cI)
- To value: 0 – we seek a solution to the equation det(A–cI) = 0
- By changing cell: B11 – i.e. we want to vary the value of c (our initial guess)
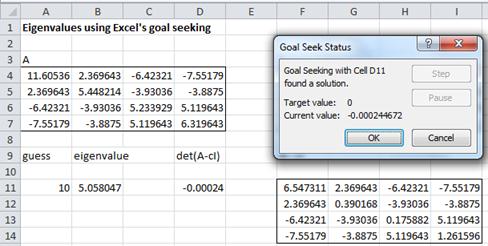
Upon pressing OK, Excel will iterate and find the solution c = 5.058047 as in Figure 2.
Figure 2 – Output from Goal Seek
Excel automatically replaces the initial guess of 10 by the solution 5.058047 and the initial value -6029.33 of det(A–cI) by a value close to our goal of zero (i.e. -0.00024). Pressing OK on the Goal Seek dialog box locks in this solution.
Multiple Solutions
We can now repeat the process by making different guesses in order to find the other 3 eigenvalues. E.g. if you make an initial guess of 20 and use Goal Seek, you will get the eigenvalue 22.95897. A guess of 0 finds the eigenvalue 0 and a guess of 1 finds the eigenvalue 0.590132.
If we had made an initial guess of 30 instead of 1, then Goal Seek would have found the solution 22.95897 again, and so you might need to make a number of guesses before finding all the eigenvalues.
Observations
Goal Seek seeks an answer within 100 iterations of its algorithm or when the accuracy of the answer is better than .001 (whichever occurs first). These default values can be overridden by selecting File > Options > Formulas (or Office Button > Options > Formulas in Excel 2007) and changing the values for Maximum Iterations and/or Maximum Change.
The Real Statistics Resource Pack contains an Eigenvalue and Eigenvector data analysis tool which automatically calculates the eigenvalues of a square matrix (and the corresponding eigenvectors). For more information, see Eigenvalues and Eigenvectors.
Solver
Excel provides another iteration tool, which is more powerful than Goal Seek, called Solver. Whereas Goal Seek enables you to find a solution to the equation f(x) ≈ a, Solver enables you to solve equations in multiple unknowns, such as f(x1,x2,…xn) ≈ a. It also allows you to find the values of x1, x2, … xn which maximizes or minimizes the value of f(x1,x2,…xn) subject to constraints.
See Solver for more details.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Cheusheva, S. (2018) How to use Goal Seek in Excel for what-if analysis
https://www.ablebits.com/office-addins-blog/2018/09/05/use-goal-seek-excel-what-if-analysis/
Hi, is there a method to find multiple possible x values that equal to one weighted average value? For example, value=Sumproduct(x1,x2,x3/y1,y2,y3)/sum(y1,y2,y3). X=value
Y= % share out of 100 for each x value.
Best
D
Derek,
There are an infinite number of such x values (unless you add additional constraints). Assuming that the y values are fixed and the weighted average X is fixed, you can assign any values you want to x1 and x2 and solve for x3.
Charles
Thanks Charles. In my sleepy state I forgot to mention that I know the target “value” and one X (price) and corresponding Y (weighting) value. The task is to find the remaining values that would result in a weighted average target “value”. I’d like a handy way to be able to do this, in excel, with any weighting I input.
Derek,
Just fill in all but one of the values with an arbitrary number and solve for the remaining value.
Charles
Sir,
If the formula and data are more the Goal seek may not give the optimum result although it will show in its calculation. generally it will calculate 100 options. can we be able to see all the options and choose the optimum solution if it is not giving the optimum solution ?
Alok,
You can change the Excel defaults for Goal Seek by selecting File > Options > Formulas
You can then change Maximum Iterations or Maximum Change.
Charles
Hi Charles,
I am trying to use solver. I need to enter 2 arguments. First i need cell X to =0 by changing percentage in cell Y. But i also need to fix cell Z to =0 as it is a function of cell X. i am doing an interest calculation on OID and DDIC and i need the OID and DDIC to =0. And as a result, i need the interest calculated from OID/DDIC to also =0. Can you help me?
Alana,
I don’t completely understand the situation that you are describing, but potentially one way to handle these sort of situations is to add constraints, which can be done in Solver.
Charles
Hi,
no problem with method 1 (goal)
but i haven’t undersood how determine the eigenvalues x1,x2,x3 at the same tim with solver:
it’s ok that you can point to ie 3 cells in the variable cells of solver…
but have you to create 3 lambda*I matrix and 3 determinant of (M-lambdaI) for calculating this?
Hi Alessandro,
As stated in the Example, this method only finds one of the eigenvalues. To find the other eigenvalues you need to use different initial guesses.
If you want to find all the eigenvalues at once you need to use other techniques. This is described on the webpage
Eigenvalues and Eigenvectors
Charles
let me know how can i find a vector such k’ that it is equal to l’x.
for example x is a 4*6 matrix as follow
1 1 0 0 1 0
1 0 1 0 0 1
1 0 1 0 1 0
1 1 0 0 0 1
Is I’ an identity matrix? If so then I’x is a 4×6 matrix and so can’t be a vector. Please clarify your questions.
Charles
Sorry it’s OK – I managed to resolve my problem. Thank you.
Hi Charles, would you be able to provide a fuller explanation of how to obtain all four eigenvalues of the matrix in your example at once using Solver? I have not been able to do this.
Regards
Tony
I also would be interested in knowing this. My thought is you could populate a random number after executing the solve, and have it continue until it produces n unique values to correspond to an n x n matrix (say, in VBA), but my guess would be there is a more direct approach to the answer, Tony. Perhaps Charles would be so kind as to reveal some of the secret sauce behind the eValues function? 😉
Victor
Hello Sir,
This is one of the easiest method of finding the co-efficients and intercepts that I have come across. Thank you for this but can you please let me know if this is as effective and accurate as finding the co-efficients and intercepts using about statistical tools such as Minitab, R or SAS
Aj,
Goal Seek and Solver tend to be sensitive to the starting value, but so far in my experience these tools have worked very well. You can tune the accuracy in Excel.
For finding regression coefficients the normal least squares method is easy and completely deterministic. For logistic regression, in addition to using Solver, I have also implemented a solution for finding the coefficients/intercepts using Newton’s Method. In my experience it gives excellent results.
Charles