Basic Concepts of Matrices

Matrices

Definition 1: An r × c matrix (also called an array) is a rectangular array (or table) with r rows and c columns. We can represent such a matrix as A = [a_ij] where 1 ≤ i ≤ r and 1 ≤ j ≤ c. Thus a_ij is the element in the ith row and jth column.

In Excel, a matrix is represented as a rectangular range. E.g. B3:C7 can be considered to be a 5 × 2 matrix.

Two matrices A = [a_ij] and B = [b_ij] are equal, denoted A = B, if they have the same size and shape (i.e. the same number of rows and columns) and all the corresponding elements are equal (i.e. a_ij = b_ij for all i, j with 1 ≤ i ≤ r and 1 ≤ j ≤ c).

Types of matrices

Definition 2: A square matrix is one where r = c. The main diagonal of a square k × k matrix A is a₁₁, …, a_kk. The trace of A is a₁₁ + … + a_kk. If all the elements in the square matrix A are 0 then the matrix is called the null matrix. If all the elements on the main diagonal are 1 and all other elements are 0 then the matrix is called an identity matrix, denoted I (or I_k to emphasize that it is a k × k identity matrix).

A triangular matrix has either all zeros in the triangular portion below the main diagonal (an upper triangular matrix) or all zeros in the triangular portion above the main diagonal (a lower triangular matrix). A diagonal matrix is one that is both an upper triangular matrix and a lower triangular matrix, i.e. all the entries off the main diagonal are zero.

Example

Example 1: Define matrix A = [a_ij] as follows:

A is a 3 × 3 square matrix whose main diagonal is 3, 5, 2. The trace of A is 3 + 5 + 2 = 10. The element in the 2^nd row and 3^rd column is a₂₃ = 4. A is an upper triangular matrix.

Vectors

Definition 3: A vector A is an r × c matrix in which either r = 1 or c = 1. If c = 1 then A is called a column vector. If r = 1 then A is called a row vector. We can represent a column vector as [a_i] where 1 ≤ i ≤ r and a row vector as [a_j] where 1 ≤  j ≤ c.

When r = c = 1 then A is called a scalar. In this case, A is the same as an ordinary number (thus [a] is considered to be the same as a).

If A is a row vector [a_i] the length of A, denoted ‖A‖ is

(and similarly for a column vector). A unit vector has length 1. To normalize a vector is to divide the vector by its length so as to yield a unit vector.

Excel Functions

Excel Functions: Excel provides the following functions. We will use the same symbol A for both the matrix and the range in the worksheet that contains the matrix.

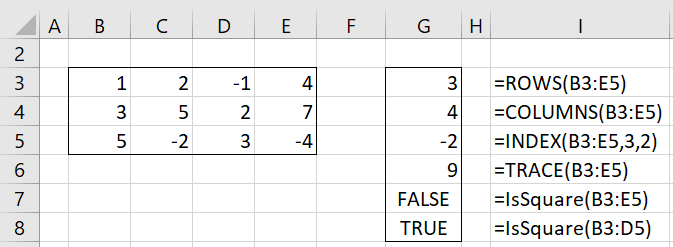
ROWS(A) = the number of rows in matrix A

COLUMNS(A) = the number of columns in matrix A

INDEX(A, i, j) = a_ij, the element in the ith row and jth column of A

Real Statistics Functions

Real Statistics Functions: The Real Statistics Resource Pack supplies the following worksheet functions

ISCELL(A) = TRUE if A is a scalar and FALSE otherwise

ISSQUARE(A) = TRUE if A is a square matrix and FALSE otherwise

LENGTH(A) = the length of matrix A; equivalent to =SQRT(SUMSQ(A))

NORM(A) = array function which outputs a normalized version of array A; i.e. = A/LENGTH(A)

DIAGONAL() = array function which outputs a square matrix whose main diagonal consists of the elements in A and which has zeros everywhere else

DIAG(A) = array function which outputs a column vector with the diagonal of A

TRACE(A) = trace of A

SSCP(A) = A^TA; i.e. = MMULT(TRANSPOSE(A),A)

IDENTITY() = outputs an identity matrix of the highlighted square shape

You can also explicitly identify the size of the identity by using the formula IDENTITY(k). In this case, the output is a k × k  identity matrix.

Examples

Example 2: Figure 1 gives some examples of these functions.

Figure 1 – Worksheet function examples

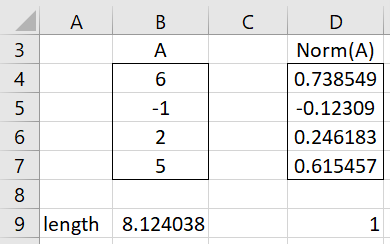
Example 3: Find the length of vector A in range B4:B7 of Figure 2 and normalize this vector.

Figure 2 – Normalizing a vector

The length is 8.124038 as shown in cell B9 of Figure 2. This can be calculated by the Excel formula =SQRT(SUMSQ(B4:B7) or the Real Statistics formula =LENGTH(B4:B7). Alternatively, you can use the array formula =SQRT(SSCP(B4:B7)).

To normalize vector A simply divide each element in A by its length, as shown in range D4:D7. This can be accomplished by placing the formula =B4/B$9.B9 in cell D4 and then highlighting the range D4:D7 and pressing Ctrl-D.  Alternatively, you can use the array formula =NORM(B4:B7).

Diagonal

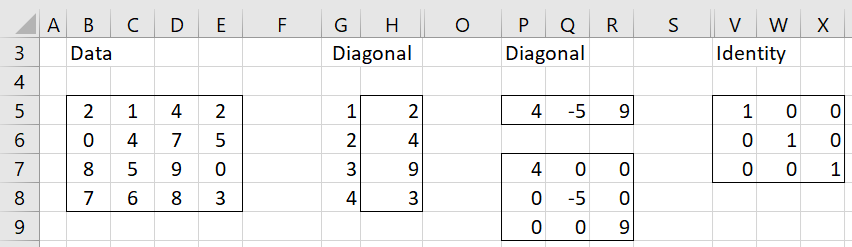
Example 4: Create a column vector with the elements on the diagonal of the matrix in the range B5:E8 of Figure 3.

Figure 3 – Diagonal of a square matrix

The result is shown in range G5:H8 using the array formula =DIAG(B5:E8). When using dynamic arrays (see Dynamic Arrays) with Excel 2021 or Excel 365, you can place the formula =TRANSPOSE(DIAG(B5:B6)) in cell H5. The transpose is required since the default for DIAG is to return a row vector.

The diagonal can be obtained in standard Excel by first creating a set of indices 1 to 4 (since the matrix is 4 × 4) as shown in range G5:G8 and then using the array formula =INDEX(A5:D8,G5:G8,G5:G8).

Excel 2021 and 365 users can insert the values in column G by placing the array formula =SEQUENCE(4) in range G5:G8). Other Excel users can obtain the same result by using the Real Statistics function SEQ in place of SEQUENCE. You can also do away with the need for the indices in column G by using the worksheet formula =INDEX(B5:E8,SEQ(4),SEQ(4)).

Example 5: Create a diagonal matrix whose main diagonal consists of the elements in range P5:R5 of Figure 3.

The result is shown in P7:R9 of Figure 3 using the array formula =DIAGONAL(P5:R5)

Identity matrix

Example 6: Create a 3 × 3 identity matrix.

This can be done by entering the formula =IDENTITY() in range V5:X7 of Figure 3. Excel 365 users can enter the dynamic array formula =IDENTITY(3) in cell V5 to obtain the same result. Of course, there is the standard Excel array formula =MUNIT(3) available in versions of Excel starting with Excel 2013.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Wikipedia (2021) Matrix (mathematics)
https://en.wikipedia.org/wiki/Matrix_(mathematics)