Refinement to significance testing
Unfortunately, for larger values of the logistic regression coefficient b, the standard error and the associated Wald statistic become inflated (see Significance testing of Logistic Regression Coefficients). This increases the probability that b will be viewed as not making a significant contribution to the model even when it does (i.e. a type II error).
To overcome this problem it is better to perform significance testing using the log-likelihood statistic, namely
where df = k – k0 and where LL1 refers to the full log-likelihood model and LL0 refers to a model with fewer coefficients (especially the model with only the intercept b0 and no other coefficients). This is equivalent to
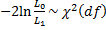Coefficient of determination
For ordinary regression the coefficient of determination
Thus R2 measures the percentage of the variance explained by the regression model. We need a similar statistic for logistic regression. We define the following three pseudo-R2 statistics for logistic regression.
Definition 1: The log-linear ratio R2 (aka McFadden’s R2) is defined as follows:
where LL1 refers to the full log-likelihood model and LL0 refers to a model with fewer coefficients (especially the model with only the intercept b0 and no other coefficients).
Cox and Snell’s R2  is defined as
where n = the sample size.
Nagelkerke’s R2 is defined as
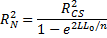Observations
Since 
The initial value L0 of L, i.e. where we only include the intercept value b0, is given by
where n0 = number of observations with value 0, n1 = number of observations with value 1 and n = n0 + n1.
As described above, the likelihood-ratio test statistic equals:
where L1 is the maximized value of the likelihood function for the full model L1, while L0 is the maximized value of the likelihood function for the reduced model. The test statistic has a chi-square distribution with df = k1 – k0, i.e. the number of parameters in the full model minus the number of parameters in the reduced model.
Example
Example 1: Determine whether there is a significant difference in survival rate between the different values of rem in Example 1 of Basic Concepts of Logistic Regression. Also, calculate the various pseudo-R2 statistics.
We are essentially comparing the logistic regression model with coefficient b to that of the model without coefficient b. We begin by calculating the L1 (the full model with b) and L0(the reduced model without b).
Here L1 is found in cell M16 or T6 of Figure 6 of Finding Logistic Coefficients using Solver.
We now use the following test:
where df = 1. Since p-value = CHISQ.DIST.RT(280.246,1) = 6.7E-63 < .05 = α, we conclude that differences in rems yield a significant difference in survival.
The pseudo-R2Â statistics are as follows:
All these values are reported by the Logistic Regression data analysis tool (see range S5:T16 of Figure 6 of Finding Logistic Coefficients using Solver).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Christensen, R. (2013)Â Logistic regression: predicting counts.
http://stat.unm.edu/~fletcher/SUPER/chap21.pdf
Wikipedia (2012)Â Logistic regression
https://en.wikipedia.org/wiki/Logistic_regression
Agresti, A. (2013)Â Categorical data analysis, 3rd Ed. Wiley.
https://mybiostats.files.wordpress.com/2015/03/3rd-ed-alan_agresti_categorical_data_analysis.pdf
Hi Charles,
when I get the value of R squared very small does that indicates my model is not good?
Will using the Newton Raphson Method fix this?
Harissa,
A small value for R-square does not necessarily mean that the model is no good.
You should get a very similar answer using the Newton Raphson method.
Charles
Then how do I test if my model is actually acceptable ? Is it by comparing the coefficients using logistic and the value of Newton Raphson? Is there any other ways we can do the Newton Raphson Methods manually on excel instead of tools?
Harissa,
1. Excellent question. How acceptable a model is depends on how you expect to use the model. E.g. if you plan to use it for forecasting, then you are probably interested in how good its forecasts are. One approach for doing this is to use part of your data for building the model and the rest for testing how good the forecasts are (comparing the values forecasted by the model with the actual test data values).
2. You can also use the Accuracy statistic calculated by the software tool. The closer to 100% the better, but is 55% good enough? This depends on a number of factors: (1) do you have a better model that is more accurate, (2) what is the cost of a wrong result, (3) what is the benefit of a correct result. Note too that a correct forecast when the real value is 0 might be much more important than a correct forecast when the real value is 1 (or vice versa).
3. The website has many examples where I have shown how to manually use the Newton-Raphson method. See the following webpage for the theory: Newton’s Method. Note that find a maximum or minimum value of a function is equivalent to find the roots of a function (namely the derivative of the original function).
Charles
Thank you Charles.
Your explanation had enlighten me .
Hope you have a nice weekend.
Harissa
Hey Charles,
Thank you for all of your work on this tool, it is amazing. I was playing around with some income data that I had dummy coded, and unexpectedly coeff b could not be calculated. It turned out that my LL1 was larger than LL0, my chi-square was negative, and that the regression produced more failures than successes. I wasn’t aware chi-square values could be negative, so is this a case of user-input error or is the tested demographic characteristics too poor to be predictive of my measured outcome?
Hello Q,
This should not happen. If you send me an Excel file with your data and test results, I will try to figure out what is going wrong.
Charles
Hi Charles
Thank you very much for the clear and concise manner in which your tutorials and examples have been presented – these have been most informative.
How would the AIC value be calculated for the “Doses of Radiation” example detailed in Example 1 of “logistic-regression/basic-concepts-logistic-regression”.
Many thanks
Anthony
Hello Anthony,
Thank you for your kind remarks.
The formula for AIC for Logistic Regression is given at
https://real-statistics.com/logistic-regression/real-statistics-functions-logistic-regression/
Charles
Hi Charles,
Please see my reply and inquiry on the relevant page – https://real-statistics.com/logistic-regression/real-statistics-functions-logistic-regression/.
Many thanks
Anthony
Hi Charles,
Thanks for all the great work and help. How would I interpret if a logistic regression model is good for predictive analytics, in the case of (as your example shows too), independent variables being significant but the pseudo r-square values being below 0.5. Is the model still useful?
Thanks!
Hi Vighnesh,
There is no reason to reject the model simply because the pseudo r-square values is below 0.5.
Charles
De
Thank you very much for the good work you are doing.
Please sir, how can i run logistic regression without intercept with real stats resource add in’
Thanks
Chyke
Basil,
The Real Statistics Resource Pack currently doesn’t support a no intercept option for Logistic Regression. I can suggest the following workaround though. Run the Logistic Regression data analysis tool and choose the Solver option. Now manually insert 0 in the intercept cell; i.e. the first coefficient under the heading Coeff. Note this is the cell that previously contained a constant value (not a formula). Next select Data > Analysis|Solver. The values in the dialog box will be those created by the Logistic Regression data analysis tool. You need to make one change and then press the OK button, namely change the range in the field called “By Changing Variable Cells” by removing the intercept cell (e.g. if the range was R4:R7, then change this range to R5:R7; here cell R4 was the cell that you changed to zero previously). I hope this helps.
Charles
Given your figure 6 output are the following statements a correct interpretation?
The results of the likelihood ratio test suggest there was statistically significant relationship between the input variable and the outcome variable at the 0.05 level of significance (chi sq (1, N=760)= 280.2421, p=6.65E-63).
The odds ratio of the input was .9928(=exp(-0.00722)) with a 95% confidence interval=(.9917,9939). This indicated that every every unit …. increased/decrease in the input variable the odds of the output variable increased/decreased by 0.9928
My understanding of your data set is weak so I’m not sure how to interpret that.
My data is pretest score and output is pass/fail class. The logisitic regression ran nicely and my model is significant.
Amy,
Yes, this seems correct.
Charles
Hi Charles,
Is there any post where the Binary logistic regression output has been interpreted. As in what does the output mean and what conclusion actions can be derived from the same.
Shri
Hi Charles,
The R-squared in linear regression is defined like so:
var(Y) = (var(Y)-var(err))/var(Y) = 1 – var(err)/var(Y)
where var(err) is derived from the absolute difference between Y and Yhat.
Why can’t we apply this definition to logistic regression where Y is the observed probability and Yhat is the estimated probability?
Wytek,
Sorry, but I have not tried to evaluate this version of R-square for logistic regression. From what I can see no one uses it. Instead they use pseudo-R-square statistics, some of which are described on my website.
Charles