Probit Regression

Basic Concepts

The logit function (see Logistic Regression Basic Concepts) maps a probability, which takes discrete values of 0 or 1, into a continuous value between -∞ and ∞.  A function with this property is called a link function. The inverse standard normal distribution function is another link function and is the basis for a regression approach similar to logistic regression, called probit regression.

Let Φ(z) represent the standard normal cumulative distribution function. Then in Excel, Φ(z) = NORM.S.DIST(z, TRUE). The inverse function Φ-1(p) = NORM.S.INV(p) is called the probit function (probit = probability unit) and plays a role similar to the logit function in probit regression. We will also use the notation for the standard normal pdf, φ(z) = NORM.S.DIST(z, FALSE).

The probit regression model takes the form

Φ-1(p) = β0 + β1x1 + β2x2 + … + βkxk + ε

where the residual random variable has a standard normal distribution, i.e. ε ∼ N(0, 1) and p = P(y = 1|X) where X = x1, x2, …, xk. This can also be expressed as Φ-1(p) = Xβ + ε where X = [xj] is a 1 × k+1 row vector of random variables (with x1 = 1) and β = [βi] is a k+1 × 1 column vector of parameters (the regression coefficients).

We estimate these population coefficients by coefficients bo, b1, …, bk based on a sample of size n whose ith element is a k+1-tuple of form Xi = xi1, xi2, …, xik. As for logistic regression, we do this by maximizing the log-likelihood statistic

log-likelihood probit regression

Once again we can use Solver or Newton’s Method to find the coefficients. In the latter case, we use the following properties.

Properties

Property 1: The maximum of the log-likelihood statistic occurs when the following k+1 equations hold for j = 0 to k.

Maximization equations LL probit

whereprobit regression value

and  xi0 = 0 and pi = Φ(z) for all i. Note too that these equations can be written in matrix form as

probit equations matrix form

Note too that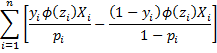

Observation: Thus, to find the values of the coefficients we need to solve the above equations. We can do this iteratively using Newton’s method (see Newton’s Method).

Property 2: Let B = [bi] be the k+1 × 1 column vector of probit regression coefficients, let Y = [yi] be the n × 1 column vector of observed outcomes of the dependent variable, let X = [xij] be the n × k+1 design matrix (as described in Multiple Regression using Matrices). Also, let P = [pi] be the n × 1 column vector of predicted values of success and V = [vij] be the n × n matrix diagonal matrix where

Diagonal matrix probit regression

on the main diagonal and zeros elsewhere. If Bo is an initial guess, and we define the following iteration

Newton iteration probit regression

then for sufficiently large m, Bm+1 ≈ Bm, and so Bm is a good approximation for the coefficient vector B.

Property 3: If B = [bi] is an estimate of the regression coefficients and V = [vij]  is the n × n matrix diagonal matrix defined as in Property 2 based on the coefficients in B, then the following matrix is a good approximation for the covariance matrix of B

Covariance matrix probit regression

and so the square root of the elements on the diagonal of this matrix are estimates of the standard errors of the regression coefficients.

See Real Statistics Probit Capabilities for how to perform probit regression in Excel using the Real Statistics Resource Pack based on the above properties.

References

Park, H. M. (2015) Regression models for binary dependent variables using Stata, SAS, R, LIMDEP, and SPSS
https://scholarworks.iu.edu/dspace/handle/2022/19740

Spermann, A. (2009) The Probit model
https://www.econometrics.uni-freiburg.de/en/teachingold/summer-term-09/materials-microeconometrics/probit_7-5-09.pdf

38 thoughts on “Probit Regression”

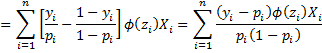
  1. IT COULD INCLUDE THE BIVARIATE PROBIT MODEL, THE MODEL IS SPECIFIED IN THE GREENE BOOK 8TH EDITION PAGE 807 IMPLEMENTATION IS NOT VERY DIFFICULT

    Reply

  6. Hi Charles

    Thanks for the step by step guide on how to use the function.

    I was actually looking for a step by step guide on how to use the probit model to forecast recession using variables like yield curve or unemployment ect.

    The trouble I’m having is the extent of the data, its not categorical and has a large time series. Then the forecasting part, I’m not exactly sure how i could have a 3,6,12 forecast on what the probability would be. Please could you run me through this step by step so that i have the correct understanding

    Regards,
    Kevin

    Reply

Leave a Comment