We now describe the Real Statistics capabilities that enable you to determine the power and minimum sample size for logistic regression.
Worksheet Functions (Normal)
Real Statistics Functions: The following functions calculate the power and sample size for binary logistic regression when the independent variable of interest is normally distributed.
LOGIT_POWER(p0, p1, odds_ratio, size, r_sq, alpha) = statistical power for binary logistic regression for the given sample size and values of p0, p1, odds_ratio, alpha and r_sq (i.e. R2).
LOGIT_SIZE(p0, p1, odds_ratio, pow, r_sq, alpha) = minimum sample size for binary logistic regression for the given power objective (pow) using the values of p0, p1, odds_ratio, alpha and r_sq.
alpha = significance level (defaults to .05), pow = power (defaults to .80) and r_sq = R2 when the other independent variables are regressed on the independent variable of interest (defaults to 0, indicating that there are no other independent variables). p0 = the probability that y = 1 when x = μx, p1 = the probability that y = 1 when x = μx,+σx and odds_ratio = the odds ratio; you need to provide a value for either p1 or odds_ratio, but not both; if both are provided then only odds_ratio will be used.
Worksheet Functions (Binary)
When the independent variable of interest takes values 0 or 1 based on a binomial distribution, the Real Statistics Resource Pack provides the following functions.
LOGIT_POWER0(p0, p1, odds_ratio, size, xpi, r_sq, alpha) = statistical power for binary logistic regression for the given sample size and values of p0, p1, odds_ratio, alpha, xpi (i.e. π) and r_sq (i.e. R2).
LOGIT_SIZE0(p0, p1, odds_ratio, pow, xpi, r_sq, alpha) = minimum sample size for binary logistic regression for the given power objective (pow) using the values of p0, p1, odds_ratio, alpha, xpi and r_sq.
alpha, pow, r_sq, odds_ratio are as for LOGIT_POWER and LOGIT_SIZE. p0 = the probability that y = 1 when x = 0 and p1 = the probability that y = 1 when x = 1; you need to provide a value for either p1 or odds_ratio, but not both; if both are provided then only p1 will be used. xpi = the portion of the sample where x = 1 (defaults to .5).
Observation
You can obtain the sample size shown in cell B12 of Figure 1 for Example 1 of Logistic Regression Sample Size (Normal) by using either of the following formulas:
=LOGIT_SIZE(B5,B6,,B4,B14,B3) or =LOGIT_SIZE(B5,,B8,B4,B14,B3)
Note that the formula =LOGIT_POWER(B5,B6,,B15,B14,B3) has value .95. If instead you use the formula =LOGIT_POWER(B5,B6,,206,B14,B3) you get the value .950145.
You can obtain the sample size shown in cell B15 of Figure 1 for Example 1 of Logistic Regression Sample Size (Binary) by using either of the following formulas:
=LOGIT_SIZE0(B5,B6,,B4,B7,0,B3) or =LOGIT_SIZE0(B5,,B9,B4,B7,0,B3)
Note that the formula =LOGIT_POWER0(B5,B6,,B15,B7,0,B3) has value .95. If instead you use the formula =LOGIT_POWER0(B5,B6,,316,B7,0,B3) you get the value .950573.
Data Analysis Tool
Real Statistics Data Analysis Tool: The Real Statistics Resource Power and Sample Size data analysis tool can be used to determine the power or estimate the minimum sample size for logistic regression.
To use this tool press Ctrl-m and select the data analysis tool from the Misc tab. Next, choose either the Logistic Regression (Normal) or Logistic Regression (Binomial) options as well as the Power or Sample Size options. After clicking on the OK button you will be presented with the appropriate dialog box. Fill in the upper part of the dialog box and press the OK button. The results will be displayed on the lower part of the dialog box.
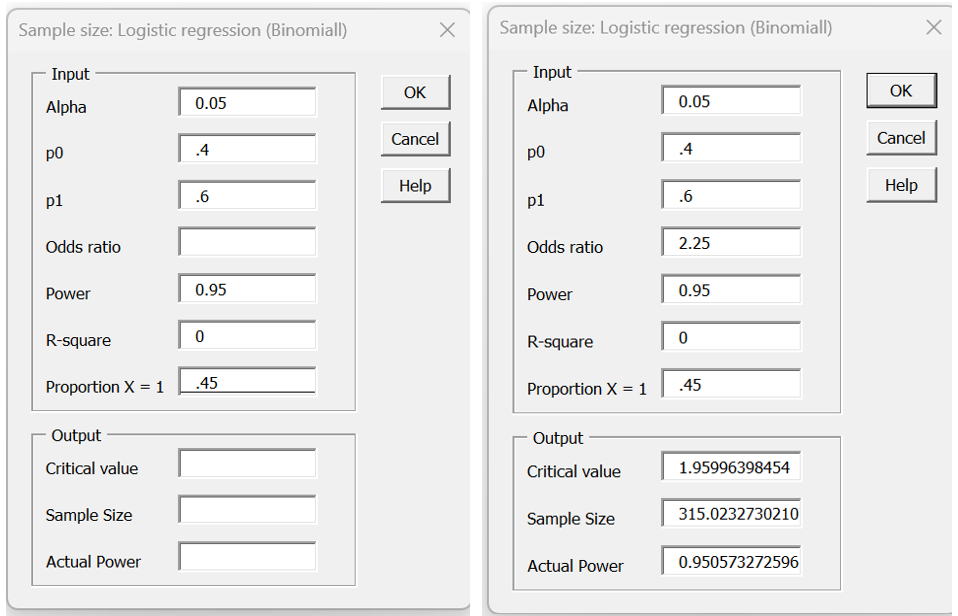
If we perform these steps for Example 1 of Logistic Regression Sample Size (Binary), then we fill in the dialog box as shown on the left side of Figure 3. When we click on the OK button, the results shown on the right side appear.
Figure 1 – Data analysis tool
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Hsieh, F. Y., Bloch, D. A., Larsen, M. D. (1998) A simple method of sample size calculation for linear and logistic regression. Statistics in Medicine
https://pubmed.ncbi.nlm.nih.gov/9699234/
Buchner, A., Erdfelder, E., Faul, F., Lang, A-G (2021) G*Power 3.1 manual
https://www.psychologie.hhu.de/fileadmin/redaktion/Fakultaeten/Mathematisch-Naturwissenschaftliche_Fakultaet/Psychologie/AAP/gpower/GPowerManual.pdf
Hsieh, F. Y. (1989). Sample size tables for logistic regression. Statistics in medicine, 8, 795-802.
http://www.statpower.net/Content/312/Handout/Hsieh%281989%29.pdf