Classification Table

Introduction

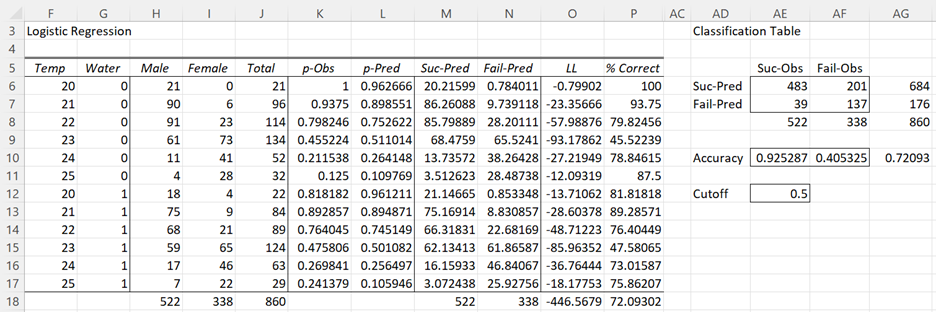
Another way of evaluating the fit of a given logistic regression model is via a Classification Table. The Real Statistics Logistic Regression data analysis tool produces this table. For Example 1 of Comparing Logistic Regression Models the table produced is displayed on the right side of Figure 1.

Figure 1 – Classification Table

The table shows a comparison of the number of successes (y = 1) predicted by the logistic regression model compared to the number actually observed and similarly the number of failures (y = 0) predicted by the logistic regression model compared to the number actually observed.

Elements of the Table

We have four possible outcomes:

True Positives (TP) = the number of cases that were correctly classified to be positive, i.e. were predicted to be a success and were actually observed to be a success

False Positives (FP) = the number of cases that were incorrectly classified as positive, i.e. were predicted to be a success but were actually observed to be a failure

True Negatives (TN) = the number of cases that were correctly classified to be negative, i.e. were predicted to be a failure and were actually observed to be a failure

False Negatives (FN) = the number of cases that were incorrectly classified as negative, i.e. were predicted to be a failure but were actually observed to be a success

The Classification Table takes the form

where PP = predicted positive = TP + FP, PN = predicted negative = FN + TN, OP = observed positive = TP + FN, ON = observed negative = FP + TN and Tot = the total sample size = TP + FP + FN + TN.

Example

For the data in Figure 1, we have

TP = 483 (cell AE6), which can be calculated by the formula =SUMIF(L6:L17,”>=”&AE12,H6:H17)

FP = 201 (cell AF6), which can be calculated by the formula =SUMIF(L6:L17,”>=”&AE12,I6:I17)

FN = 39 (cell AE7), which can be calculated by the formula =H18-AE6

TN = 137 (cell AF7), which can be calculated by the formula =I18-AF6

Here cell AE12 contains the cutoff value of .5. Predicted values (in column L) greater than or equal to this value are classified as positive (i.e. predicted to be a success), those less than this value are classified as negative (i.e. predicted to be a failure). TP is simply the sum of all the values in column H whose predicted probabilities in column L are ≥ .5.

The cutoff value is specified in the Logistic Regression dialog box (see for example Figure 4 of Finding Logistic Regression Coefficients using Excel’s Solver).

Note that FP is the type I error and FN is the type II error described in Hypothesis Testing.

Other Concepts

We now can define the following:

True Positive Rate (TPR), aka Sensitivity = TP/OP = 483/522 = .925287 (cell AE10)

True Negative Rate (TNR), aka Specificity = TN/ON = 137/338 = .405325 (cell AF10)

Accuracy (ACC) = (TP + TN)/Tot = (483 + 137) / 860 = .720930 (cell AG10)

False Positive Rate (FPR) = 1 – TNR = FP/ON = 201/338 = .594675

Positive Predictive Value (PPV) = TP/PP = 483/684 = .70614

Negative Predictive Value (NPV) = TN/PN = 137/176 = .77841

The overall accuracy of the logistic regression model is a measure of the fit of the model. For Example 1 this is .720930, which means that the model is estimated to give an accurate prediction 72% of the time.

Note that the accuracy of each outcome is given in column P of Figure 1. E.g. the accuracy of Temp = 21 and Water = 0 is 93.75% (cell P7), which can be calculated by the formula

=100*IF(L7>=$AE$12,H7/J7,I7/J7)

The total accuracy of the model (cell P18) can then be calculated by the formula

=SUMPRODUCT(P6:P17,J6:J17)/J18

The value of cell P18 is .720930, which is the same value we obtained in the classification table (cell AG10).

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Kaggle (2023) Classification table – confusion matrix. Logistic regression using R
https://www.kaggle.com/code/benroshan/part-8-logistic-regression-using-r

MedCalc (2023) ROC curves
https://www.medcalc.org/manual/roc-curves.php