Spectral Decomposition

Spectral Decomposition Theorem

Property 1: Let A be a symmetric n×n matrix, then A has a spectral decomposition A = CDC^T where C is an n×n matrix whose columns are unit eigenvectors C₁, …, C_n corresponding to the eigenvalues λ₁, …, λ_n of A and D is the n×n diagonal matrix whose main diagonal consists of λ₁, …, λ_n.

Proof: We prove that every symmetric n×n matrix is orthogonally diagonalizable by induction on n. The property is clearly true for n = 1. We assume that it is true for any n × n symmetric matrix and show that it is true for an n+1 × n+1 symmetric matrix A.

Let λ be any eigenvalue of A (we know by Property 1 of Symmetric Matrices that A has n+1 real eigenvalues) and let X be a unit eigenvector corresponding to λ. Thus AX = λX, and so X^TAX = X^TλX = λ(X^TX) = λ(X ∙ X) = λ, showing that λ = X^TAX.

By Property 3 of Linear Independent Vectors, we can construct a basis for the set of all n+1 × 1 column vectors which includes X, and so using Theorem 1 of Orthogonal Vectors and Matrices (Gram-Schmidt), we can construct an orthonormal basis for the set of n+1 × 1 column vectors which includes X. Now define B to be the matrix whose columns are the vectors in this basis excluding X. By Property 4 of Orthogonal Vectors and Matrices, B is an n+1 × n orthogonal matrix.

Note that (B^TAB)^T = B^TA^TB^T = B^TAB since A is symmetric. This shows that B^TAB is a symmetric n × n matrix, and so by the induction hypothesis, there is an n × n diagonal matrix E whose main diagonal consists of the eigenvalues of B^TAB and an orthogonal n × n matrix P such B^TAB = PEP^T. Now define the n+1 × n matrix Q = BP. Note that by Property 5 of Orthogonal Vectors and Matrices Q is orthogonal.

Now define the n+1 × n+1 matrix C whose first row is X and whose remaining rows are those of Q, i.e. C = [X, Q]. We now show that C is orthogonal. First we note that since X is a unit vector, X^TX = X ∙ X = 1. Since the columns of B along with X are orthogonal, X^TB_j= X ∙ B_j = 0 for any column B_j in B, and so X^TB = 0, as well as B^TX = (X^TB)^T = 0. Finally since Q is orthogonal, Q^TQ = I.

Now

This completes the proof that C is orthogonal. We next show that Q^TAQ = E.

Next we need to show that Q^TAX = X^TAQ = 0. Since

since A is symmetric, it is sufficient to show that Q^TAX = 0.

As we saw above, B^TX = 0. Also, since λ is an eigenvalue corresponding to X, AX = λX. Thus,

Now

 Defining

it follows that C^TAC = D, and so

Note that at each stage of the induction, the next item on the main diagonal matrix of D is an eigenvalue of A and the next column in C is the corresponding eigenvector and that this eigenvector is orthogonal to all the other columns in C.

Observation: The spectral decomposition can also be expressed as A = .

Example

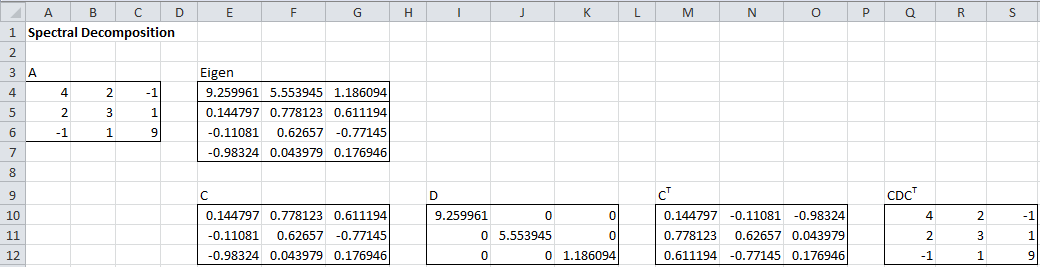
Example 1: Find the spectral decomposition of the matrix A in range A4:C6 of Figure 1.

Figure 1 – Spectral Decomposition

We calculate the eigenvalues/vectors of A (range E4:G7) using the supplemental function eVECTORS(A4:C6). Matrix C (range E10:G12) consists of the eigenvectors of A and matrix D (range I10:K12) consists of the square roots of the eigenvalues. You can check that A = CDC^T using the array formula

=MMULT(E10:G12,MMULT(I10:K12,M10:O12))

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack provides the following function:

SPECTRAL(R1, iter): returns a 2n × n range whose top half is the matrix C and whose lower half is the matrix D in the spectral decomposition of CDC^T of A where A is the matrix of values in range R1.

Here iter is the number of iterations in the algorithm used to compute the spectral decomposition (default 100).

Data Analysis Tool

Real Statistics Data Analysis Tool: The Spectral Factorization option of the Real Statistics Matrix Operations data analysis tool also provides the means to output the spectral decomposition of a symmetric matrix.

Observation

As we have mentioned previously, for an n × n matrix A, det(A – λI) is an nth degree polynomial of form (-1)ⁿ  (x – λ_i) where λ₁, …., λ_n are the eigenvalues of A. If all the eigenvalues are distinct then we have a simpler proof for Property 1 (see Property 4 of Symmetric Matrices). But as we observed in Symmetric Matrices, not all symmetric matrices have distinct eigenvalues. This motivates the following definition.

Multiplicity

Definition 1: The (algebraic) multiplicity of an eigenvalue is the number of times that eigenvalue appears in the factorization (-1)ⁿ  (x – λ_i) of det(A – λI).

Property 2: For any eigenvalue λ of a square matrix, the number of independent eigenvectors corresponding to λ is at most the multiplicity of λ.

Proof: Suppose λ₁ is an eigenvalue of the n × n matrix A and that B₁, …, B_k are k independent eigenvectors corresponding to λ₁. By Property 3 of Linear Independent Vectors, there are vectors B_k+1, …, B_n such that B₁, …, B_n is a basis for the set of n × 1 vectors. Now let B be the n × n matrix whose columns are B₁, …, B_n. Since B₁, …, B_n are independent, rank(B) = n and so B is invertible. By Property 9 of Eigenvalues and Eigenvectors we know that B^-1AB and A have the same eigenvalues, and in fact, they have the same characteristic polynomial.

Now consider AB. The first k columns take the form AB₁, …, AB_k, but since B₁, …, B_k are eigenvectors corresponding to λ₁, the first k columns are λB₁, …, λB_k. It now follows that the first k columns of B^–1AB consist of the vectors of the form D1, …, D_k where D_j consists of λ₁ in row j and zeros elsewhere. This means that the characteristic polynomial of B^–1AB has a factor of at least (λ – λ₁)^k, i.e. the multiplicity of B^–1AB, and therefore A, is at least k.

Property 3: For each eigenvalue λ of a symmetric matrix there are k independent (real) eigenvectors where k equals the multiplicity of λ, and there are no more than k such eigenvectors.

Proof: By Property 1, any symmetric n×n matrix A has n orthonormal eigenvectors corresponding to its n eigenvalues. By Property 2 of Orthogonal Vectors and Matrices, these eigenvectors are independent. This shows that the number of independent eigenvectors corresponding to λ is at least equal to the multiplicity of λ. But by Property 5 of Symmetric Matrices, it can’t be greater than the multiplicity of λ, and so we conclude that it is equal to the multiplicity of λ.

By Property 1 of Symmetric Matrices, all the eigenvalues are real and so we can assume that all the eigenvectors are real too.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Golub, G. H., Van Loan, C. F. (1996) Matrix computations. 3rd ed. Johns Hopkins University Press

Searle, S. R. (1982) Matrix algebra useful for statistics. Wiley

Perry, W. L. (1988) Elementary linear algebra. McGraw-Hill

Fasshauer, G. (2015) Linear algebra.
https://math.iit.edu/~fass/532_handouts.html

Lambers, J. (2010) Numerical linear algebra
https://www.yumpu.com/en/document/view/41276350