QR Factorization Continued

Partial Orthogonal Factorization

If A is an m × n matrix with m > n and A = QR is the QR factorization of A with Q an m × n matrix and R an n × n matrix, then QQ^T = I while Q^TQ ≠ I. Thus, Q is only partially orthogonal. We also say that A = QR is a partial QR factorization.

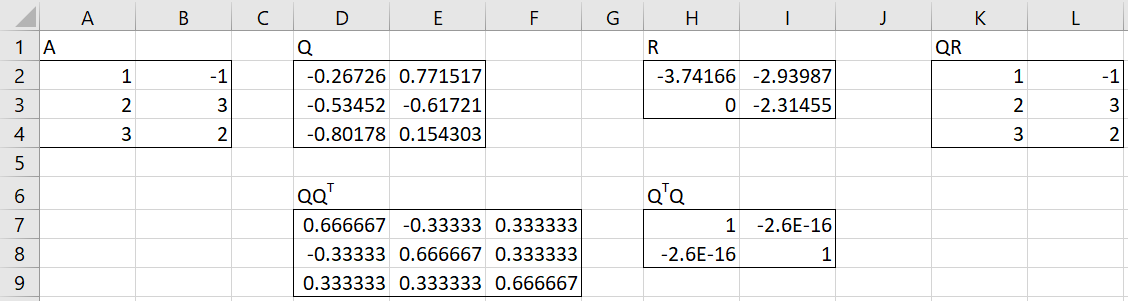
For example, in Figure 1 we display the partial QR factorization of the 3 × 2 matrix A. As expected, Q^TQ = I but QQ^T ≠ I.

Figure 1 – Partial QR factorization for 3 × 2 matrix

Similarly, if A is an m × n matrix with m < n and A = QR is the QR factorization of A with Q an m × n matrix and R an n × n matrix, then QQ^T = I while Q^TQ ≠ I. Thus, once again, Q is only partially orthogonal. We also say that A = QR is a partial QR factorization.

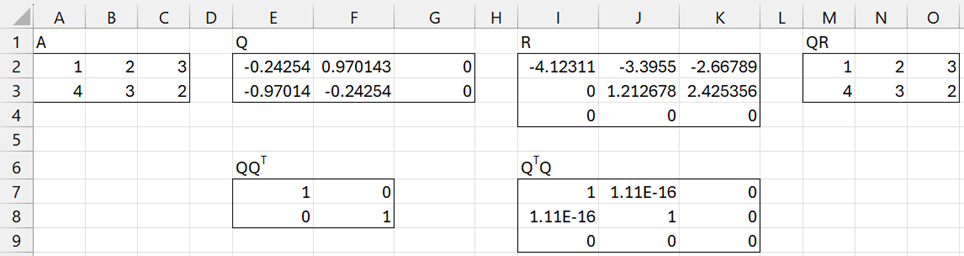
For example, in Figure 2 we display the partial QR factorization of the 2 × 3 matrix A. As expected, QQ^T = I but Q^TQ ≠ I.

Figure 2 – Partial QR factorization for 2 × 3 matrix

if m ≥ n then Q^TQ = I. Thus, if A is a square matrix, then A = QR where Q is orthogonal, i.e. Q^TQ = I and QQ^T = I. If A is not a square matrix, then Q is only partially orthogonal.

Full QR Factorization

There is another version of the QR factorization of A, which we will refer to as the full QR factorization. 

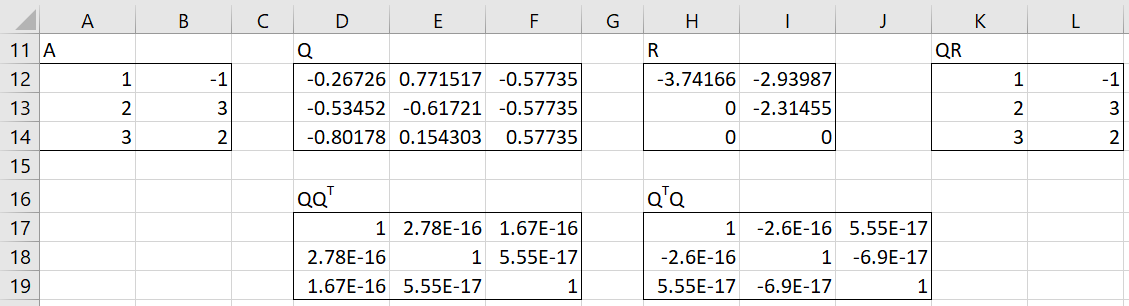
If A is an m × n matrix with m > n, then A = QR is the (full) QR factorization of A with Q an m × m matrix and R an upper triangular m × n matrix. This time QQ^T = I and Q^TQ = I, and so Q is indeed orthogonal.

Figure 3 displays the full QR factorization of the A matrix from Figure 1.

Figure 3 – (Full) QR factorization

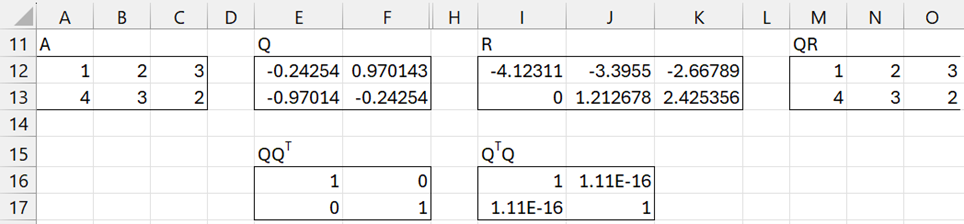
If A is an m × n matrix with m < n, then A = QR is the (full) QR factorization of A with Q an m × m matrix and R an upper triangular m × n matrix. This time QQ^T = I and Q^TQ = I, and so Q is indeed orthogonal.

Figure 4 displays the full QR factorization of the A matrix from Figure 2.

Figure 4 – Full QR factorization for 2 × 3 matrix

QR Factorization for square matrices

Note that for square matrices the full and reduced QR factorizations are the same.

Worksheet Functions

For non-square matrices, the worksheet functions QRFactorR, QRFactorQ, and QRFactor described in QR Factorization return the partial versions of the QR factorizations, To obtain the full QR factorizations, we need to use the following worksheet functions.

Real Statistics Functions: The Real Statistics Resource Pack provides the following array functions, where R1 is an m × n array or cell range.

QRFullR(R1, prec): outputs the m × n upper triangular array R for which A = QR where A is the matrix in R1.

QRFullQ(R1, prec): outputs the m × m array Q for which A = QR where A is the matrix in R1.

QRFull(R1, prec): outputs an m × m+n array. The first m columns of the output is Q and the next n columns of the output is R where A = QR and A is the matrix in range R1.

For square matrices, QRFullR, QRFullQ, and QRFull return the same values as QRFactorR, QRFactorQ, and QRFactor.

The partial QR factorization in Figure 1 can be calculated by using =QRFactorQ(A2:B4) in range D2:E4 and =QRFactorR(A2:B4) in range H2:I3.

The full QR factorization in Figure 3 can be calculated by using =QRFullQ(A12:B14) in range D12:F14 and =QRFullR(A12:B14) in range H12:I14. Note that the output from =QRFull(A12:B14) looks like the contents of range D12:I14 with column G removed.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Golub, G. H., Van Loan, C. F. (1996) Matrix computations. 3rd ed. Johns Hopkins University Press

Searle, S. R. (1982) Matrix algebra useful for statistics. Wiley

Perry, W. L. (1988) Elementary linear algebra. McGraw-Hill

Fasshauer, G. (2015) Linear algebra.
https://math.iit.edu/~fass/532_handouts.html

Lambers, J. (2010) Numerical linear algebra
https://www.yumpu.com/en/document/view/41276350