The pseudo-inverse A+ (aka the Moore-Penrose inverse) of an m × n matrix A is an extension of the inverse of a square matrix to non-square matrices and to singular (i.e. non-invertible) square matrices.
Full-rank case
We first consider the case where the matrix A has full rank, and so the rank of A = min(m,n).
The pseudo-inverse matrix A+ is an n × m matrix with the following properties:
- If m ≥ n, then ATA is invertible and A+ = (ATA)-1AT and so A+A = I, i.e. A+ is a left inverse of A.
- If m ≤ n, then AAT is invertible and A+ = AT(AAT)–1 and so AA+ = I, i.e. A+ is a right inverse of A.
- If A is invertible then A+ = A-1
Note that given a series of linear equations expressed as AX = C, we can obtain a solution via X = A+AX = A+C
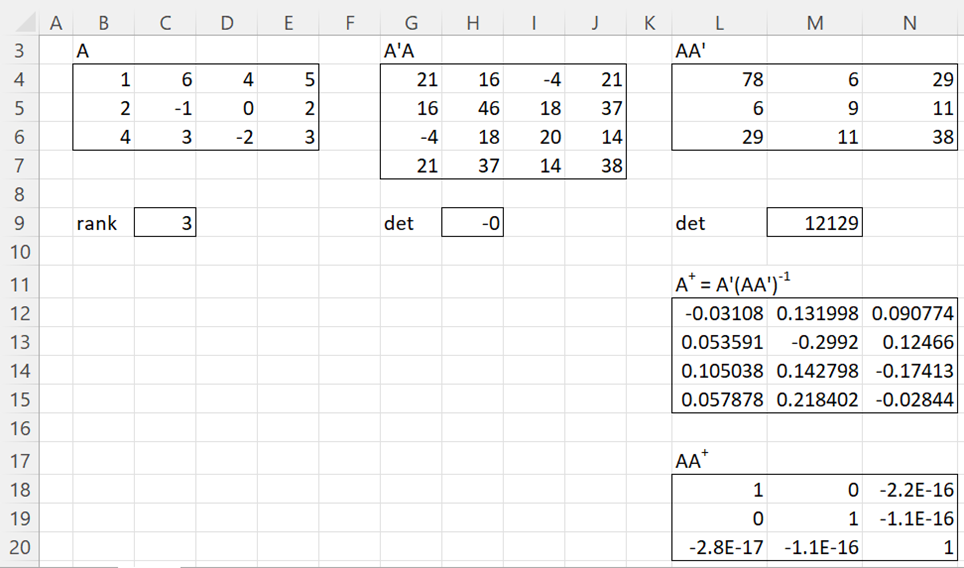
Example 1: Find the pseudo-inverse for the matrix in range B4:E6 of Figure 1.
The result is shown in range L12:N15 of Figure 1.
Figure 1 – Pseudo-inverse for matrix of full rank
We note A is of full rank since MRANK(B4,E6) = 3. We also note that A’A is not invertible (det = 0), and so we use AAT to calculate the pseudo-inverse (as expected since m < n). Finally, we see that AA+ = I, as shown in range L18:N20. Note that while A+ is a right inverse, it is not a left inverse (A+A ≠ I).
Worksheet Function (Full-Rank)
Real Statistics Function: The Real Statistics Resource Pack provides the following function which can be used when R1 contains a full-rank matrix.
PseudoInv(R1, 0): outputs an array that is the pseudo-inverse of the matrix in array R1.
We can calculate the pseudo-inverse of A in Example 1 by using the formula PseudoInv(B4:E6,0) in range L12:N15 of Figure 1.
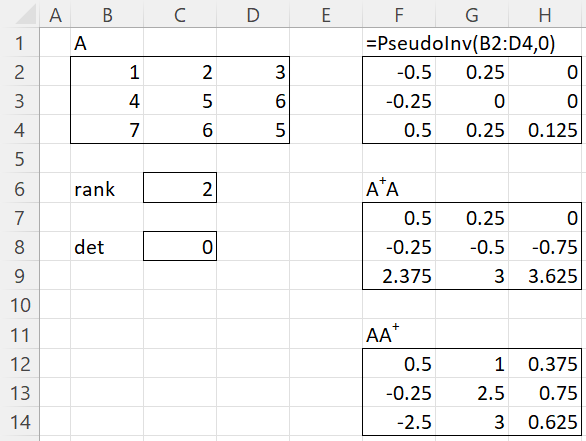
Example 2: Find the pseudo-inverse for the matrix in range B2:D4 of Figure 2.
Figure 2 – Non-full-rank matrix
We see from Figure 2 that the rank of the matrix is 2, which means that the matrix is not of full rank, and so the approach described above is not appropriate. In fact, we also see that the pseudo-inverse generated by the formula =PseudoInv(B2:D4,0) is not a left or right inverse. Since A is a square matrix, its pseudo-inverse would be the same as its ordinary inverse, provided A were invertible. But A is not invertible since det(A) = 0.
This doesn’t mean that A doesn’t have a pseudo-matrix. It just means that we need a different method to find it.
Using the SVD method
Suppose A = UDVT is the Singular Value Decomposition (SVD) of A. Then the pseudo-inverse A+ = VD+UT where D+ is the diagonal matrix formed by taking the reciprocal of each non-zero element in D, leaving the zeros in place, and then transposing the resulting matrix.
Note that A+A = (VD+UT)(UDVT) = VD+DVT = VVT = I provided D+D = I, which will be the case if A is of full rank.
Thus, the SVD method is an alternative approach to finding the pseudo-inverse for a matrix of full rank. It turns out that the SVD approach works even for matrices, not of full rank, but first, we need to modify the definition of a pseudo-inverse since in this case, the matrix won’t have a right or left inverse.
Matrix A+ is the pseudo-inverse of A provided the following four properties hold:
- AA+A = A
- A+AA+ = A+
- (AA+)+ = AA+
- (A+A)+ = A+A
Note that if A is of full rank, then either AA+ = I or A+A = I, and so it is easy to see that all four properties hold.
It turns out that any matrix has a pseudo-inverse as defined above, and that this pseudo-inverse is unique. We can use the SVD approach described above to find this pseudo-inverse.
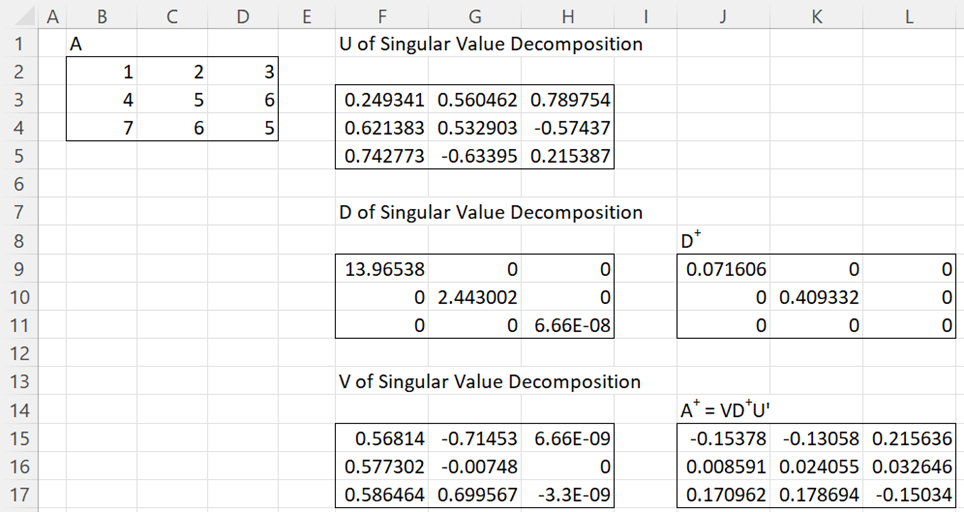
Example 3: Find the pseudo-inverse for the matrix in range B2:D4 of Figure 2 using the SVD approach.
The result is shown in range J15:L17 of Figure 3.
Figure 3 – SVD approach
Worksheet Function (SVD)
Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet function.
PseudoInv(R1, iter, prec): outputs an array that is the pseudo-inverse of the matrix in array R1 using the SVD approach.
iter (default 200) and prec (default 0.00001).
We can obtain the pseudo-inverse in Example 3 by using the array formula =PseudoInv(B2:D4) in range J15:L17 of Figure 3.
Gaussian Elimination Approach
When a matrix is not of full rank, we can use the following approach instead of the SVD approach. Calculate the matrix AAT and use Gaussian elimination to reduce this matrix to row echelon form via the worksheet formula =ELIM(AAT). Finally, eliminate any final rows containing all zeros to obtain the matrix we will call P.
- Repeat step 1 on the matrix ATA to obtain the matrix R.
- Calculate Q = RT
- Calculate the matrix M = (PAQ)-1
- Finally, calculate the pseudo-inverse A+ = QMP
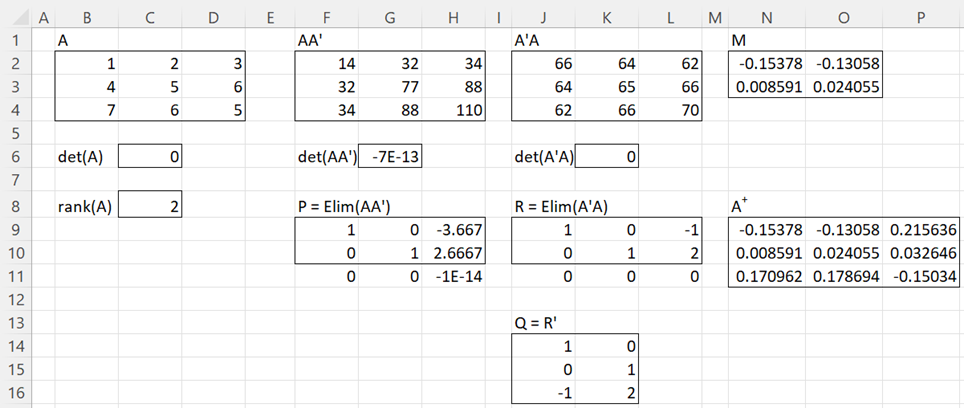
Example 4: Repeat Example 3 using the above procedure.
This is shown in Figure 4. The result shown in range N9:P11 is the same as that obtained using the SVD approach, as shown in Figure 3.
Figure 4 – Pseudo-inverse using Gaussian elimination
Worksheet Function (Gaussian Elimination)
Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet function.
PseudoInv(R1, -1, prec): outputs an array that is the pseudo-inverse of the matrix in array R1 using the SVD approach.
The Gaussian elimination approach is employed when the second argument in PseudoInv is negative. Here prec is a small positive numeric value (default .00001). During Gaussian elimination, any value whose absolute value is less than or equal to prec is treated as zero.
We can obtain the pseudo-inverse in Example 4 by using the array formula =PseudoInv(B2:D4) in range N9:P11 of Figure 4.
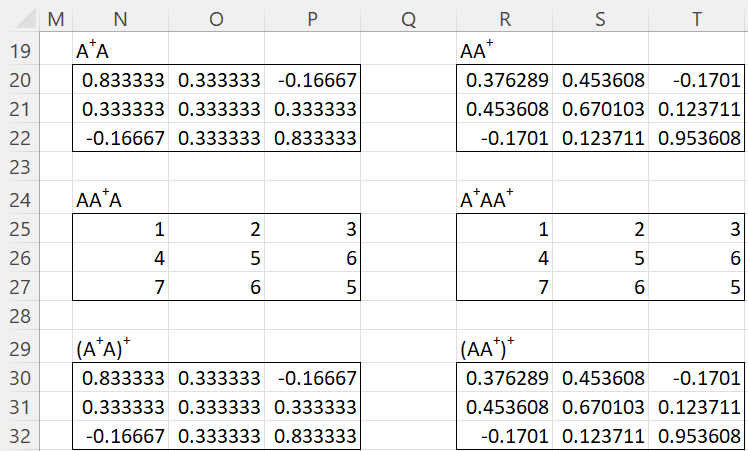
Example 5: Check to see that the criteria for a pseudo-inverse are met for Example 4 (as well as Example 3).
We can see from Figure 5 that these four criteria are met. We also see that the pseudo-inverse is not a right inverse nor a left inverse.
Figure 5 – Checking the criteria for a pseudo-inverse
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
de Wet, R. (2021) Pseudoinverse calculator
https://www.omnicalculator.com/math/pseudoinverse
Wikipedia (2021) Penrose inverse
https://en.wikipedia.org/wiki/Moore%E2%80%93Penrose_inverse