Positive definite and semidefinite matrices
Definition 1: An n × n symmetric matrix A is positive definite if for any n × 1 column vector X ≠ 0, XTAX > 0. A is positive semidefinite if for any n × 1 column vector X, XTAX ≥ 0.
Observation: Note that if A = [aij] and X = [xi], then
If we set X to be the column vector with xk = 1 and xi = 0 for all i ≠ k, then XTAX = akk, and so if A is positive definite, then akk > 0, which means that all the entries in the diagonal of A are positive. Similarly, if A is positive semidefinite then all the elements in its diagonal are non-negative.
Properties
Property 1: If B is an m × n matrix, then A = BTB is symmetric
Proof: If B = [bij] is an m × n matrix then A = BTB = [akj] is an n × n matrix where akj = . A is symmetric since by Property 1 of Matrix Operations, AT = (BTB)T = BT(BT)T = BTB = A.
Observation: If X = [xi] is an m × 1 column vector, then XTX = .
Property 2: If B is an m × n matrix, then A = BTB is positive semidefinite.
Proof: As we observed in Property 1, A is a symmetric n × n matrix. For any n × 1 column vector X, BX is an m × 1 column vector [ci] where ci = , and so
Property 3: If B is an m × n matrix of rank n where n ≤ m, then A = BTB is a positive definite matrix.
Proof: From the proof of Property 2, we know that XTAX = for any n × 1 column vector X. Now let X be any non-null n × 1 column vector. If all the
are zero, then BX = 0. But by Property 3 of Matrix Rank, if follows that X = 0, which is a contradiction. Since BX ≠ 0, at least one of the ci ≠ 0, and so
> 0, which means that XTAX =
> 0, and so A is positive definite.
Equivalent positive semidefinite properties
Property 4: The following are equivalent for a symmetric n × n matrix A:
- A is positive semidefinite
- There is a matrix U such that A = UTU
- All the eigenvalues of A are non-negative
Proof: Assume (c) and show (b). Since A is symmetric, by Property 1 of Spectral Decomposition, A has a spectral decomposition A = CDCT where D consists of the eigenvalues λ1, …, λn of A. By assumption these are all non-negative, and so there exists the diagonal matrix D½ whose main diagonal consists of , …,
. Since D½D½ = D, we have
and so the desired matrix is U = (CD½)T.
Assume (b) and show (a). Let X be any n × 1 column vector. Then
![]() Assume (a) and show (c). Let A be positive semidefinite and let X be an eigenvector corresponding to eigenvalue λ. Since A is positive semidefinite, XTAX ≥ 0. Since X is an eigenvector corresponding to λ, AX = λX, and so 0 ≤ XTAX = XTλX = λXTX. Finally, since XTX = ||X|| > 0, it follows that λ ≥ 0.
Assume (a) and show (c). Let A be positive semidefinite and let X be an eigenvector corresponding to eigenvalue λ. Since A is positive semidefinite, XTAX ≥ 0. Since X is an eigenvector corresponding to λ, AX = λX, and so 0 ≤ XTAX = XTλX = λXTX. Finally, since XTX = ||X|| > 0, it follows that λ ≥ 0.
Equivalent positive definite properties
Property 5: The following are equivalent for a symmetric n × n matrix A:
- A is positive definite
- There is an invertible matrix U such that A = UTU
- All the eigenvalues of A are positive
Proof: Assume (c) and show (b). Since A is symmetric, by Property 1 of Spectral Decomposition, A has a spectral decomposition A = CDCT where D consists of the eigenvalues λ1, …, λn of A. By assumption these are all positive, and so there exists the diagonal matrix D½ whose main diagonal consists of , …,
. Since D½D½ = D, we have
and so the desired matrix is U = (CD½)T provided we can show that U is invertible. Now C is an orthogonal matrix and so C-1 = CT. Since D½ is a diagonal matrix det D½ = the product of the elements on the diagonal. Since all the elements on the main diagonal are positive, it follows that det D½ ≠ 0, and so D½ is invertible. Thus U is invertible with inverse ((D½)-1CT)T, which is CE, where E = the diagonal matrix whose main diagonal consists of the elements , …,
Assume (b) and show (a). Let X be any n × 1 column vector. Then
If ||UX||2 = 0 then UX = 0. Since U is invertible, X = U-1UX = 0, which is a contradiction. Thus XTAX = ||UX||2 > 0.
Assume (a) and show (c). Let A be positive definite and let X be an eigenvector corresponding to eigenvalue λ. Since A is positive definite, XTAX > 0. Since X is an eigenvector corresponding to λ, AX = λX, and so 0 < XTAX = XTλX = λXTX. Finally, since XTX = ||X|| > 0, it follows that λ > 0.
Determinant
Property 6: The determinant of a positive definite matrix is positive. Furthermore, a positive semidefinite matrix is positive definite if and only if it is invertible.
Proof: The first assertion follows from Property 1 of Eigenvalues and Eigenvectors and Property 5. The second follows from the first and Property 4 of Determinant of a Square Matrix.
Observation: A positive semidefinite matrix A is symmetric, and so it makes sense to speak about the spectral decomposition of A.
Square root of a positive semidefinite matrix
Definition 2: If A is a positive semidefinite matrix, then the square root of A, denoted A½, is defined to be the n × n matrix CD½CT where C is as defined in Definition 1 of Symmetric matrices and D½ is the diagonal matrix whose main diagonal consists of , …,
.
Property 7: If A is a positive semidefinite matrix, then A½ is a symmetric matrix and A = A½A½
Proof:
Since a diagonal matrix is symmetric, we have
![]() Covariance matrix
Covariance matrix
Property 8: Any covariance matrix is positive semidefinite. If the covariance matrix is invertible then it is positive definite.
Proof: We will show the proof for the sample covariance n × n matrix S for X. The proof for a population matrix is similar. Note that
![]() where X = [xij] is a k × n matrix such that for each i, {xij : 1 ≤ j ≤ n} is a random sample for the random variable xi. Now let Y be any n x 1 column vector. Thus
where X = [xij] is a k × n matrix such that for each i, {xij : 1 ≤ j ≤ n} is a random sample for the random variable xi. Now let Y be any n x 1 column vector. Thus
Now the following matrices can be represented as a dot product, which evaluate to the same scalar ci
which shows that any covariance matrix is positive semidefinite. The second assertion follows from Property 6.
Observation: A consequence of Property 4 and 8 is that all the eigenvalues of a covariance (or correlation) matrix are non-negative real numbers.
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack provides the following array function, where R1 is a k × k array.
MSQRT(R1): Produces a k × k array which is the square root of the matrix represented by range R1
Example
Example 1: Find the square root of the matrix in range A4:C6 of Figure 1.
Figure 1 – Square root of a matrix
Range A9:C9 contains the eigenvalues of matrix A and range A10:C12 contains the corresponding eigenvectors (which are repeated as matrix C). These can be calculated using eVECTORS(A4:C6). D½ is a diagonal matrix whose main diagonal consists of the square roots of the eigenvalues.
The square root of A is therefore given in range I4:K6, calculated by the array formula
=MMULT(E4:G6,MMULT(E9:G11,E14:G16))
The same result can be achieved using the array formula =MSQRT(A4:C6).
Note that the spectral decomposition A = CDCT is captured by the array formula
=MMULT(E4:G6,MMULT(DIAGONAL(A9:C9),E14:G16))
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Golub, G. H., Van Loan, C. F. (1996) Matrix computations. 3rd ed. Johns Hopkins University Press
Searle, S. R. (1982) Matrix algebra useful for statistics. Wiley
Perry, W. L. (1988) Elementary linear algebra. McGraw-Hill
Fasshauer, G. (2015) Linear algebra.
https://math.iit.edu/~fass/532_handouts.html
Lambers, J. (2010) Numerical linear algebra
https://www.yumpu.com/en/document/view/41276350
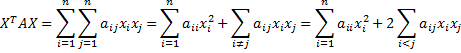
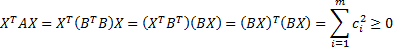

Hello Charles
Is there a process using the Real Statistics Resource Pack to transform a correlation matrix that has one or more negative eigenvalues into a matrix that is Positive Definite? The end goal is to be able to do a Cholesky Decomposition for use in generating correlated random returns for Monte Carlo analysis. I am “cleaning” the matrix in excel using spectral decomposition, but it is cumbersome, and in some cases, the changes to individual correlation values can be in excess of 4%, which seems like a fairly material change to me. I would appreciate your insight.
Hello Steve,
A correlation matrix can only have positive eigenvalues and so no transformation is necessary.
If the correlation matrix is based on data that has some missing elements (where the matrix is based on pairwise correlations ignoring missing data), then the resulting matrix is not really a correlation matrix and may not be positive definite.
Charles
Thank you for your reply, Charles. And, I echo the feedback of so many others on how much I appreciate your site and the capabilities of Real Stats.
Charles, is there any reason why a correlation matrix would show up with eVECTORS generating all positive eigenvalues (i.e., positive semidefinite), whereas a covariance matrix created with the exact same underlying data shows up with eVECTORS generating a couple of negative eigenvalues? I have tried several different “iter” parameters (default, 1,000, 10,000 for an 11 x 11 matrix).
My takeaway from Property 8 above would be that if the covariance matrix was a valid one, it should be generating all positive eigenvalues.
Victor,
If you send me an Excel file with an example where you get negative eigenvalues from a covariance matrix I will try to figure out what is going on. See the Contact Us webpage for my email address.
Charles
Just sent you an email earlier today, Charles. Thanks very much.
Victor,
I received your email and will respond shortly.
Charles
What do you mean in Property 8 when you say:
“Now the following are the same scalar c”?
Thanks
Hi… I am trying to understand proof of Property 3: what do you mean ‘ …but by Property 4 of Matrix Operations, if follows that X = 0’ … Could you explain it in more detail? thank you
Property 4 of Matrix Operations is the wrong reference. It should be Property 3 of Rank of Matrix. I have corrected the referenced webpage. Thanks for bringing this error to my attention.
Charles
hello, lead me please
If M is spd matrix show that none of its diagonal elements can be nonpositive.
Thank you
Since A is a positive definite nxn matrix (for some n), for any n × 1 non-zero column vector XTAX > 0. Try selecting X such that all the entries are zero except for one entry which is 1.
Charles