Orthogonal Vectors and Matrices

Orthogonal Vectors

As we observed in Matrix Operations, two non-null vectors X = [x_i] and Y = [y_i] of the same shape are orthogonal if their dot product is 0, i.e. 0 = X ∙ Y = x_i y_i. Note that if X and Y are n × 1 column vectors, then X ∙ Y = X^TY = Y^TX, while if X and Y are 1 × n row vectors, then X ∙ Y = XY^T = YX^T. It is easy to see that (cX) ∙ Y = c(X ∙ Y), (X + Y) ∙ Z = X ∙ Z + Y ∙ Z, X ∙ X =  > 0 and other similar properties of the dot product.

Property 1: If A is an m × n matrix, X is an n × 1 vector and Y is an m × 1 vector, then

(AX) ∙ Y = X ∙ (A^TY)

Proof: (AX) ∙ Y = (AX)^TY = (X^TA^T)Y = X^T(A^TY) = X ∙ (A^TY)

Property 2: If X₁, …, X_m are mutually orthogonal vectors, then they are independent.

Proof: Suppose X₁, …, X_m are mutually orthogonal and let = 0. Then for any j, 0 = X_j ∙ = = c_j (X_j  ∙ X_j) since X_j ∙ X_i = 0 when i ≠ j. Thus, c_j (X_j  ∙ X_j) = 0. But since X_j ∙ X_j > 0, it follows that c_j = 0. Since this is true for any j, X₁, …, X_m are independent.

Property 3: Any set of n mutually orthogonal n × 1 column vectors is a basis for the set of n × 1 column vectors. Similarly, any set of n mutually orthogonal 1 × n row vectors is a basis for the set of 1 × n row vectors.

Proof: This follows by Corollary 4 of Linear Independent Vectors and Property 2.

Observation: Let C_j be the jth column of the identity matrix I_n. As we mentioned in the proof of Corollary 4 of Linear Independent Vectors, it is easy to see that for any n, C₁, …, C_n forms a basis for the set of all n × 1 column vectors. It is also easy to see that the C₁, …, C_n are mutually orthogonal.

We next show that any set of vectors has a basis consisting of mutually orthogonal vectors.

Gram-Schmidt Theorem

Property 4: Suppose X₁, …, X_m are independent n × 1 column vectors. Then we can find n × 1 column vectors V₁, …, V_m which are mutually orthogonal and have the same span.

Proof: We show how to construct the V₁, …, V_m from the X₁, …, X_m as follows.

Define V₁, …, V_m as follows:

Proof: We first show that the V_k are mutually orthogonal by induction on k. The case where k = 1 is trivial. Assume that V₁, …, V_k are mutually orthogonal. To show that V₁, …, V_k+1 are mutually orthogonal, it is sufficient to show that V_k+1 ∙ V_i = 0 for all i where 1 ≤ i ≤ k. Using the induction hypothesis that V_j ∙ V_i = 0 for 1 ≤ j ≤ k and j ≠ i and V_i ∙ V_i ≠ 0 (since V_i ≠ 0), we see that

This completes the proof that V₁, …, V_m are mutually orthogonal. By Property 2, it follows that V₁, …, V_m are also independent.

We next show that the span of V₁, …, V_k is a subset of the span of X₁, …, X_k  for all k ≤ m. The result for k = 1 is trivial. We assume the result is true for k and show that it is true for k + 1. Based on the induction hypothesis, it is sufficient to show that V_k+1 can be expressed as a linear combination of X₁, …, X_k+1. This is true since by definition

and by the induction hypothesis, all the V_j can be expressed as a linear combination of the  X₁, …, X_k.

By induction, we can now conclude that the span of V₁, …, V_m is a subset of the span of X₁, …, X_m, and so trivially V₁, …, V_m are elements in the span of X₁, …, X_m But since the V₁, …, V_m are independent, by Property 3 of Linear Independent Vectors, we can conclude that the span of V₁, …, V_m is equal to the span of X₁, …, X_m.

Corollary 1: For any closed set of vectors we can construct an orthogonal basis

Proof: By Corollary 1 of Linear Independent Vectors, every closed set of vectors V has a basis. In fact, we can construct this basis. By Property 4, we can construct an orthogonal set of vectors that spans the same set. Since this orthogonal set of vectors is independent, it is a basis for V.

Orthonormal Vectors

Definition 1: A set of vectors is orthonormal if the vectors are mutually orthogonal and each vector is a unit vector.

Corollary 2: For any closed set of vectors we can construct an orthonormal basis

Proof: If V₁, …, V_m is the orthogonal basis, then Q₁, …, Q_m is an orthonormal normal basis where

Observation: The following is an alternative way of constructing Q₁, …, Q_m (which yields the same result).

Define V₁, …, V_m and Q₁, …, Q_m from X₁, …, X_m as follows:

Orthonormal Matrices

Definition 2: A matrix A is orthogonal if A^TA = I.

The following property is an obvious consequence of this definition.

Property 5: A matrix is orthogonal if and only if all of its columns are orthonormal.

Property 6: If A is an m × n orthogonal matrix and B is an n × p orthogonal then AB is orthogonal.

Proof: If A and B are orthogonal, then

(AB)^T(AB) = (B^TA^T)(AB) = B^T(A^TA)B = B^TIB = B^TB = I 

Example

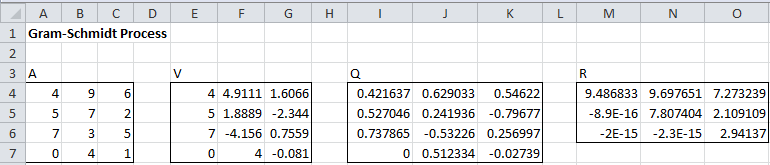
Example 1: Find an orthonormal basis for the three column vectors which are shown in range A4:C7 of Figure 1.

Figure 1 – Gram Schmidt Process

The columns in matrix Q (range I4:K7) are simply the normalization of the columns in matrix V. E.g., the third column of matrix Q (range K4:K7) is calculated using the array formula G4:G7/SQRT(SUMSQ(G4:G7)). The columns of V are calculated as described in Figure 2.

Figure 2 – Formulas for V in the Gram Schmidt Process

The orthonormal basis is given by the columns of matrix Q. That these columns are orthonormal is confirmed by checking that Q^TQ = I by using the array formula =MMULT(TRANSPOSE(I4:K7),I4:K7) and noticing that the result is the 3 × 3 identity matrix.

We explain the matrix R from Figure 1 in Figure 3 and in Example 2 below. Also, we explain how to calculate the matrix R in Example 1 of QR Factorization.

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack provides the following array function which implements the Gram-Schmidt process in Excel.

GRAM(R1, n, prec): returns an m × n  array whose columns form an orthonormal basis whose span includes the span of the columns in R1. In executing the algorithm, values less than or equal to prec are considered to be equivalent to zero (default 0.0000001)

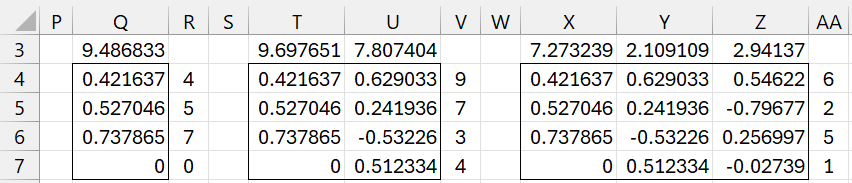
We can use the function =GRAM(A4:C7) to obtain the results shown in range I4:K7. Note that each column in A4:C7 can be expressed as a linear combination of the basis vectors in I4:K7. E.g. as can be seen from Figure 3, the third vector in the original matrix (repeated in column Y of Figure 3) can be expressed as the linear combination AA4:AA7 = X3*X4:X7 + Y3*Y4:Y7 + Z3:Z4:Z7.

Figure 3 – Creating an orthonormal basis

Note that the vectors in columns X, Y, Z are the same as the basis vectors shown in columns I, J, K of Figure 1. Also, note that the scalar multipliers in row 3 of Figure 3 are the same as the non-zero elements in the R matrix shown in Figure 1. Actually, we can obtain the same result for Q (with less chance for roundoff error) by using the =QRFactorQ(A4:C7) as described in QR Factorization. Also, note that the R matrix can be calculated by =QRFactorR(A4:C7).

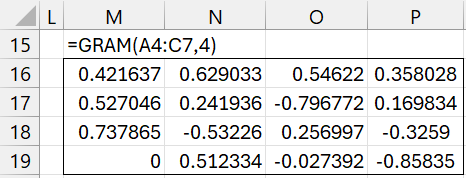
We can obtain a basis for all vectors with 4 elements by augmenting the original three vectors with the vector (1, 0, 0, 0)^T obtaining the basis shown in Figure 4 by using the formula =GRAM(A4:C7,4).

Figure 4 – Expanding the basis

Properties of Orthogonal Matrices

Property 7: If A is an orthogonal square matrix, then

1. A^T = A^-1
2. AA^T = I
3. A^T is orthogonal
4. det A = ±1 (the converse is not necessarily true)

Proof:

a) Since A^T is a left inverse of A, by Property 5 of Rank of a Matrix, A^T is the inverse of A
b) This follows from (a)
c) This follows from (b) since (A^T)^TA^T = AA^T = I
d) By Property 1 of Determinants and Linear Equations, |A|² = |A| ∙ |A| = |A^T| ∙ |A|= |A^TA| = |I| = 1. Thus |A|=±1.

Property 8: A square matrix is orthogonal if and only if all of its rows are orthonormal.

Proof: By Property 5 and 7b.

Multiplying a vector X by an orthogonal matrix A has the effect of rotating or reflecting the vector. Thus we can think of X as a point in n-space which is transformed into a point AX in n-space. Note that the distance between the point X and the origin (i.e. the length of vector X) is the same as the distance between AX and the origin (i.e. the length of vector AX), which can be seen from

Also, the multiplication of two vectors by A also preserves the angle between the two vectors, which is characterized by the dot product of the vectors (since the dot product of two unit vectors is the cosine of this angle), as can be seen from

 

Note too that A represents a rotation if det A = +1 and a reflection if det A = -1.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Golub, G. H., Van Loan, C. F. (1996) Matrix computations. 3rd ed. Johns Hopkins University Press

Searle, S. R. (1982) Matrix algebra useful for statistics. Wiley

Perry, W. L. (1988) Elementary linear algebra. McGraw-Hill

Fasshauer, G. (2015) Linear algebra.
https://math.iit.edu/~fass/532_handouts.html

Lambers, J. (2010) Numerical linear algebra
https://www.yumpu.com/en/document/view/41276350