Basic Concepts
Definition: An (upper) Hessenberg matrix is a square matrix where all the entries below the first diagonal below the main diagonal are zeros. Similarly, a lower Hessenberg matrix is a square matrix where all the entries above the first diagonal above the main diagonal are zeros.
A square matrix A is similar to a Hessenberg matrix if there exists a Hessenberg matrix H as well as an orthogonal matrix Q such that A = QTHQ (this is called a Hessenberg decomposition or Hessenberg factorization of A). In this case, QQT = QTQ = I and so Q–1 = QT.
A tridiagonal matrix is a square matrix that is both upper and lower Hessenberg (i.e. non-zero entries can only occur on the main diagonal or the first diagonal above or below the main diagonal).
Property 1: All square matrices are similar to a Hessenberg matrix.
Property 2: All symmetric matrices are similar to a tridiagonal matrix.
Worksheet Functions
Real Statistics Functions: The following functions are provided in the Real Statistics Resource Pack. Here R1 is an n × n square array and prec is a small non-negative number (default 0.000000000001) where any value ≤ prec is considered to be equivalent to zero).
HessH(R1, prec): returns a Hessenberg matrix that is similar to the square matrix in R1.
HessQ(R1, prec): returns a matrix Q for which if H = HessH(R1, prec) then R1 = QTHQ.
HESS(R1, prec): returns a 2n × n array for the n × n array R1 such that the first n rows are H and the last n rows are Q where H = HessH(R1, prec) and Q = HessQ(R1, prec)
Eigenvalues and eigenvectors
The eigenvalues of a square matrix are the same as those of a Hessenberg matrix that it is similar to. Since Hessenberg matrices are simpler than other square matrices, to find the eigenvalues of a matrix it is usually worthwhile to first find a similar Hessenberg matrix and then find the eigenvalues of that matrix. Also, if A = QTHQ is a Hessenberg decomposition of A and V is an eigenvector of H that corresponds to the eigenvalue λ (of H), then QV is an eigenvector of A that corresponds to the eigenvalue λ (of A).
Property 1 is constructive; in particular, we can find a similar Hessenberg matrix by using Householder reflections in a manner similar to that described for constructing a QR decomposition.
Hessenberg Decomposition Example
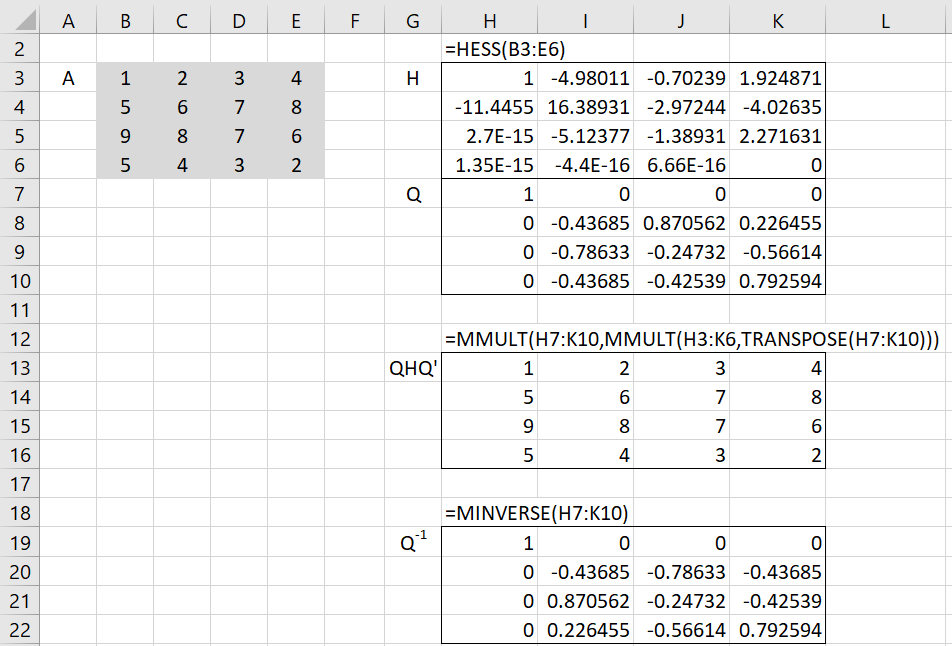
Example 1: Find the Hessenberg decomposition for the matrix in range B3:E6 of Figure 1.
Figure 1 – Hessenberg decomposition
We find the decomposition by placing the array formula =HESS(B3:E6) in range H3:K10. Note that A = QHQT, as can be seen in range H13:K16. We also see that H is an upper triangular matrix and Q-1 = QT.
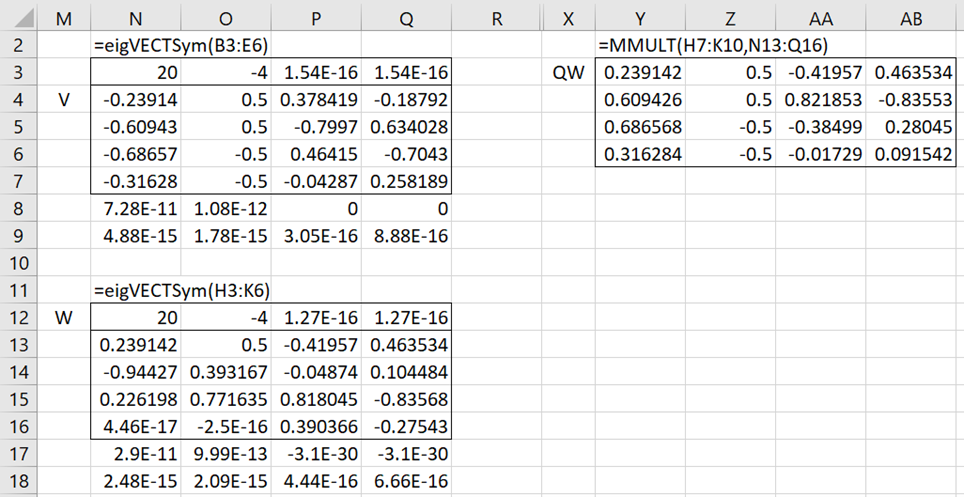
From Figure 2, we see that 20, -4, 0, 0 are the eigenvalues of matrix A, with corresponding eigenvectors V shown in the columns of range N4:Q7. We see that matrix H has the same eigenvalues as A, with eigenvectors W. The matrix product of QW shown on the right side of Figure 2 also yields four eigenvectors of A. The first two of these eigenvectors match those in range N4:Q7. While the last two eigenvectors don’t match exactly, they are alternative eigenvectors corresponding to the two zero eigenvalues.
Figure 2 – Eigenvectors
Tridiagonal Decomposition Example
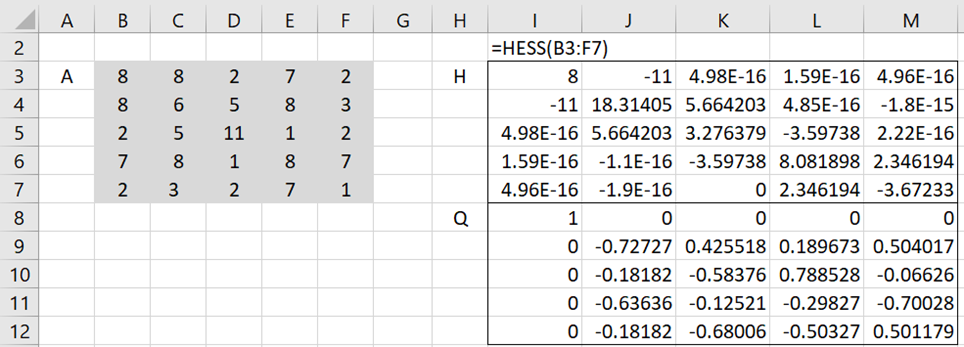
Example 2: Find the tridiagonal decomposition for the symmetric matrix in range B3:F7 of Figure 3.
Figure 3 – Tridiagonal decomposition
Using the array =HESS(B3:F7), we calculate the H and Q matrices as shown in Figure 3. Note that this time H is a tridiagonal matrix.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Golub, G. H., Van Loan, C. F. (1996) Matrix computations. 3rd ed. Johns Hopkins University Press
Searle, S. R. (1982) Matrix algebra useful for statistics. Wiley
Perry, W. L. (1988) Elementary linear algebra. McGraw-Hill
Fasshauer, G. (2015) Linear algebra.
https://math.iit.edu/~fass/532_handouts.html
Lambers, J. (2010) Numerical linear algebra
https://www.yumpu.com/en/document/view/41276350