Eigenvalue and eigenvector functions

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following functions to calculate the eigenvalues and eigenvectors of a square matrix.

eigVAL(R1, order, check, iter, prec): returns a 3 × n array, where n = the number of rows/columns in the square array R1. The first two rows of the output consist of the real and imaginary parts of the n eigenvalues of the square matrix A corresponding to the data in R1. The third row of the output consists of the values det(A−λI) for each eigenvalue λ.

eigVECT(R1, order, check, iter, prec): returns an n+4 × n array, where n = the number of rows/columns in the square array R1. The first two rows of the output consist of the real and imaginary parts of the n eigenvalues of the square matrix A corresponding to the data in R1. Below each real eigenvalue λ in the first two rows (i.e. in the columns where the second row is zero) is an n × 1 unit eigenvector corresponding to λ. In the second-to-last row of the output are the values det(A−λI). In the last row of the output, below each real eigenvalue λ and eigenvector X is the value max {b_i: i = 1 to n} where B = AX− λX.

Function arguments

If order = TRUE or -1 (default) then the eigenvalues are arranged in descending order based on the absolute values of their real part. If order = FALSE or 0 then the eigenvalues are arranged in descending order of their real parts. Finally, if order = +1 then the eigenvalues are not sorted.

If check = TRUE (default), then the output is as described above, if check = FALSE then only the first two rows of the output are returned for eigVAL and the last two rows of the output are not returned for eigVECT.

If iter > 0 then an additional binary divide-and-conquer algorithm is applied to the real eigenvalues to improve their precision (i.e. potentially reduce the values in the last row of eigVAL or second-to-last row of eigVECT). iter = the maximum number of iterations of this algorithm (default 200) and prec is the desired precision (default .00000001).

Note that if the eigenvalues are distinct, then the eigenvectors will be mutually independent. In fact, they will be mutually orthogonal and so the matrix of these eigenvectors will be orthonormal. Otherwise, repeated eigenvalues may not have distinct eigenvectors.

Real Eigenvalues

The following related array functions are also available. These support square matrices with only real eigenvalues.

eigVALReal(R1, order, check, iter, prec)

eigVECTReal(R1, order, check, iter, prec)

The output is the same as for eigVAL and eigVECT except that the second row of the output (containing the imaginary part of the eigenvectors) is omitted since it is presumed that all the eigenvalues are real and so don’t have an imaginary part.

If R1 has a non-real eigenvalue, then the first row of the output will contain the value “imag” for each non-real eigenvalue. Since such eigenvalues occur in pairs (λ = u±vi), you should expect an even number of such entries. 

Symmetric Matrices

In addition, the following array functions are also available to support symmetric square matrices.

eigVALSym(R1, order, check, iter, prec)

eigVECTSym(R1, order, check, iter, prec)

The output for eigVALSym is identical to that from eigVALReal. The output from eigVECTSym is identical to that from eigVECTReal except that all the eigenvectors are mutually orthogonal, including those corresponding to repeated eigenvalues (i.e. those whose multiplicity > 1).  Symmetric matrices can only have real eigenvalues and eigenvectors, and they cannot have any defective eigenvectors. If R1 has any imaginary eigenvalues, then an error value is returned.

Actually, eigVECTSym can be used even with nonsymmetric matrices as long as there are no imaginary eigenvalues. The eigenvectors that are output will be mutually orthogonal as long as there are no defective eigenvalues.

Legacy Functions

Earlier releases of the Real Statistics Resource Pack supported the following functions. These functions can still be used, although we now implement them via the eigVALSym and eigVECTSym functions described above.

eVALUES(R1, iter, order) = eigVALSym(R1, order, TRUE, iter)

eVECTORS(R1, iter, order) = eigVECTSym(R1, order, TRUE, iter)

eVECT(R1, iter, order) = eigVECTSym(R1, order, TRUE, iter)

Examples

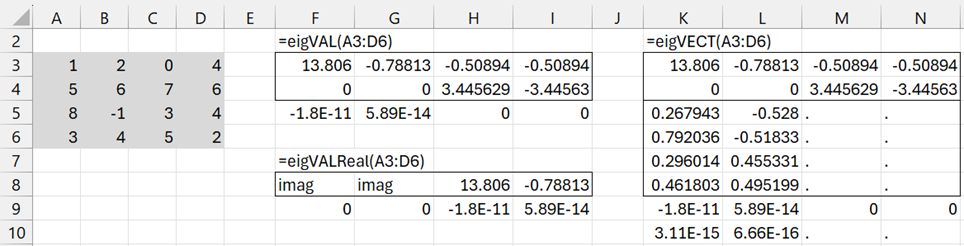
Example 1: Find the eigenvalues and eigenvectors for the matrix in range A3:D6 of Figure 1.

Figure 1 – eigVAL and eigVECT

We see from F3:I4  of Figure 1 that there are two real eigenvalues 13.806 and -.78813 and two complex eigenvectors -.50894 ± 3.445629i. The values close to zero in range F5:I5 confirm that these are the eigenvalues. The unit eigenvectors corresponding to the two real eigenvalues are shown in ranges K5:K8 and L5:L8. That these are valid eigenvectors is confirmed by the two near-zero values in cells K10 and K11.

Note: If you need the complex eigenvectors that correspond to the complex eigenvalues you need to use the ZEigVECT function. See Complex Eigenvalues and Eigenvectors.

Example with real eigenvalues

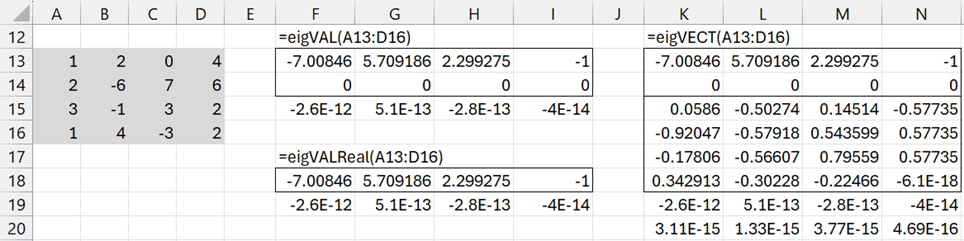
Example 2: Find the eigenvalues and eigenvectors for the matrix in range A13:D16 of Figure 2.

Figure 2 – All real eigenvalues

This time we see from Figure 2 that all the eigenvalues are real and therefore all the corresponding eigenvectors are real too.

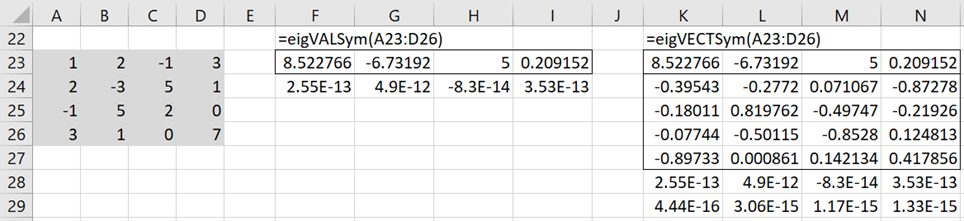
Example 3: Find the eigenvalues and eigenvectors for the matrix in range A23:D26 of Figure 3.

Figure 3 – Symmetric matrix

Since the matrix is symmetric all the eigenvalues and eigenvectors will be real. We use the eigVALSym and eigVECTSym array functions to calculate these values as shown in Figure 3.

Repeated Eigenvalues

In all three of these examples, there are four distinct eigenvalues. The situation is a bit more complicated when one or more of the eigenvalues is repeated. Click here for an example where an eigenvalue has a multiplicity greater than one.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Golub, G. H., Van Loan, C. F. (1996) Matrix computations. 3rd ed. Johns Hopkins University Press

Searle, S. R. (1982) Matrix algebra useful for statistics. Wiley

Perry, W. L. (1988) Elementary linear algebra. McGraw-Hill

Fasshauer, G. (2015) Linear algebra.
https://math.iit.edu/~fass/532_handouts.html

Lambers, J. (2010) Numerical linear algebra
https://www.yumpu.com/en/document/view/41276350