Complex eigenvalues and eigenvectors continued

This webpage contains additional information about real and complex eigenvectors and is a continuation of the discussion started at Complex Eigenvalues and Vectors.

Eigenvalues and eigenvectors in Excel format

Excel uses text to represent complex numbers. E.g. the first eigenvalue in Figure 3 of  Complex Eigenvalues and Vectors is represented as “3.933133+0.930767i”.

Real Statistics Function: The Real Statistics Resource Pack provides the following function that outputs real and complex eigenvalues and eigenvectors in Excel format from a square matrix with real values.

IMEigVECT(R1, ndigits, check, iter, prec): returns an n+4 × n array, where n = the number of rows/columns in the square array R1. The output is the same as that produced by ZEigVECT except that now the Excel format for complex numbers is used.

Since the output uses Excel’s complex number notation, sometimes the resulting text string can be long and somewhat unreadable. To address this issue, a ndigits parameter is used to round off the real and imaginary parts of a complex number to ndigits decimal places (default 4).

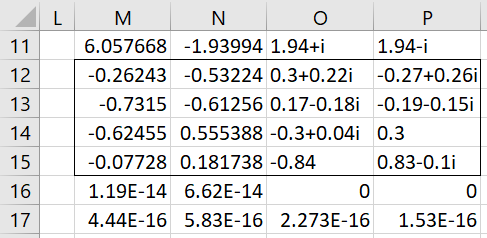
The output from the formula IMEigVECT(B3:E6,2) is shown in Figure 1.

Figure 1 – Eigenvalues/vectors in Excel format

The first two columns of the output, corresponding to real eigenvalues, use numeric format, while the last two columns, corresponding to complex eigenvalues, use Excel’s complex number format.  Note that the results are the same as those shown in Figure 2 of Complex Eigenvalues and Vectors except that the formatting is different. Also, note that the complex numbers have been rounded to two decimal places. E.g. O12 contains the text string “0.3+0.22i” instead of “0.300208+0.224596” (see range Q4:R4 from Figure 2 of Complex Eigenvalues and Vectors).

Repeated Eigenvalues

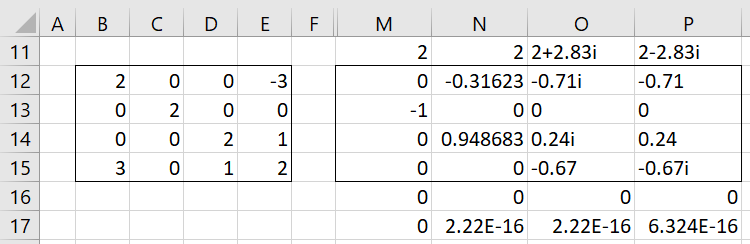
The eigenvalues for the matrix on the left side of Figure 2 consist of two repeated real eigenvalues (2 and 2) and one pair of complex eigenvalues, as can be seen from the output of ZMEigVECT(B12:E15) on the right side of the figure.

Figure 2 – Repeated eigenvalues

Since eigenvectors for all the eigenvalues are displayed in the output, we observe that the repeated eigenvalue is not defective.

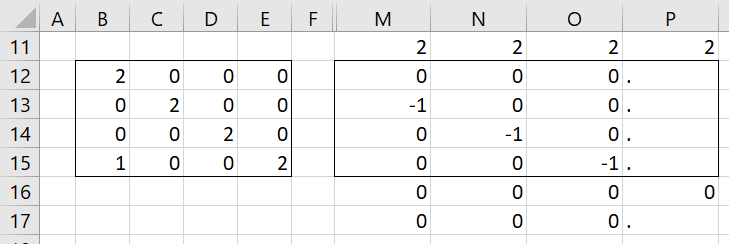
The matrix on the left side of Figure 3 has one eigenvalue, namely 2, repeated four times. As can be seen from the right side of the figure, there are three independent eigenvectors, but the fourth eigenvector is missing (and so is replaced by “.”).

Figure 3 – Defective real eigenvalue

Thus, 2 is a defective eigenvalue. Note that any of the three eigenvectors in columns M, N and O (or any scalar multiple of any of them) can be used in range P12:P15, but there is not a fourth such vector that is independent of the other three.

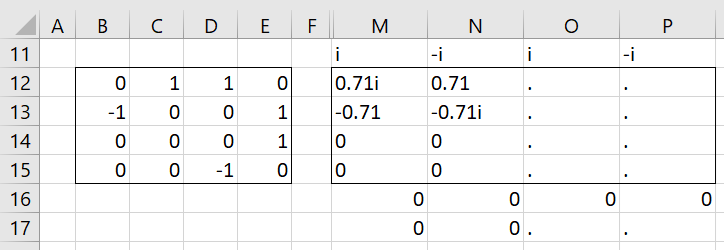
The matrix on the left side of Figure 4 has two complex eigenvalues, namely i and ‑i, repeated twice. As can be seen from the right side of the figure, there are two independent eigenvectors, but the third and fourth eigenvectors are missing (and so are replaced by “.”).

Figure 4 – Repeated complex eigenvalues

Thus, i and -i are defective eigenvalues. Note that the two eigenvectors in columns M and N can be copied into range O12:P15, but there isn’t a pair of such vectors that are independent of the other two.

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack provides the following function that outputs real and complex eigenvectors for repeated eigenvalues in Real Statistics format from a square matrix with real values.

ZEigMultVECT(R1, re, im, prec): returns the eigenvectors for the eigenvalue re + im*i, which is presumably a repeated eigenvalue. Similar to eigMultVECT (see Eigenvectors for Repeated Eigenvalues). The key difference is that both real and complex eigenvalues (and eigenvectors) are supported.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2021) Eigenvalues and eigenvectors
https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors

Brenner, S. C., Kaup, D. J. (1999) Introduction to complex numbers
https://control.dii.unisi.it/sistdin-SI/complex.pdf