Statistical Power and Sample Size

Basic Concepts

The following four measures are interrelated:

• sample size
• effect size (which is related to variance)
• alpha (significance level)
• power (which is related to beta)

In particular, for a given sample size and effect size, the lower the alpha the higher the beta (i.e. the lower the power) and vice versa.

Objectives

Usually, we are interested in the following two consequences of the interaction of the above four parameters:

Calculate the minimum sample size (a priori): Prior to conducting an experiment, it is important to determine the minimum sample size necessary to achieve the desired statistical power based on an assumed alpha and estimated effect size. The effect size is based on similar experiments, theoretical considerations, or as a last resort commonly used guidelines (e.g. those of Cohen described in Standardized Effect Size).

Calculate the power of a test (post hoc): After conducting a specific statistical test with a selected alpha and sample size, you can determine the effect size, and then calculate the power of the test. If the power is at least as large as some other target value (usually .80 or .90), then you can be confident that the power of the test is sufficient to detect the effect (i.e. produce a significant result if the effect is larger than this effect size). But if the power is lower than this value then you need to consider repeating the experiment with a larger sample if this is practical.

Example

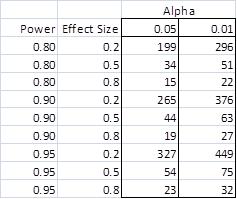
The table in Figure 1 gives some idea of how the minimum sample size varies based on the alpha, effect size, and power parameters (a priori analysis). The example is for the two-tailed Student’s t-test for a single sample (see One Sample t Test) where d = .2 represents a small effect, d = .5 represents a medium effect and d = .8 represents a large effect.

Figure 1 – Sample size requirements

E.g. the first line of the table shows that a sample of size 199 or more is needed to detect an effect of size d = 0.2 with power 1 – β = 0.80 and α = 0.05. To achieve power of 90% requires a sample of size 265, but if you only need to detect an effect of size .5, then you only need a sample of size 44 to achieve 90% power.

Resources

The Real Statistics Resource Pack provides several worksheet functions for carrying out both a priori and post hoc tests in Excel. We illustrate these via numerous examples throughout this website (see, for example, Power and Sample Size, Statistical Power of the t-Tests, Power for One-way ANOVA, etc.).

The Real Statistics Resource Pack also provides a data analysis tool that calculates power and sample size requirements for thirteen statistical tests. Click here to access a description of this data analysis tool.

If you need power and sample size capabilities beyond those provided by the Real Statistics Resource Pack there are software programs that can do this for you. One such program, G*Power, is available for free online.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Howell, D. C. (2010) Statistical methods for psychology, 7th Ed. Wadsworth. Cengage Learning
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf

Zar. J. H. (2010) Biostatistical analysis 5^th Ed. Pearson
https://bayesmath.com/wp-content/uploads/2021/05/Jerrold-H.-Zar-Biostatistical-Analysis-5th-Edition-Prentice-Hall-2009.pdf

Faul, F., Erdfelder, E., Buchner, A., & Lang, A. G. (2009). Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41, 1149-1160.
http://link.springer.com/article/10.3758/BRM.41.4.1149

STAT (2015) Power and sample size reference manual, release 13
http://www.stata.com/manuals13/pss.pdf