Basic Concepts
As described in Dealing with Familywise Error, if you perform k statistical tests, you would need to use a corrected significance level of
α* = 1 – (1 – α)1/k
on each test to achieve an overall significance level of α. This is called the Dunn-Sidàk correction. Since α* ≈ α/k, an α/k correction, called the Bonferroni correction, is commonly used instead since it is easier to calculate.
Note that these estimates are the worst-case since they assume that the individual null hypotheses are independent. If when one of these hypotheses is true, then one, or more, of the other hypotheses is likely to also be true, then the familywise error may indeed be lower.
If we choose a test that tries to handle multiple null hypotheses at the same time, then we say that such a test is conservative when the actual familywise error rate of the test is less than the target significance level alpha, while if the familywise error rate is more than alpha, then the test is liberal.
Example
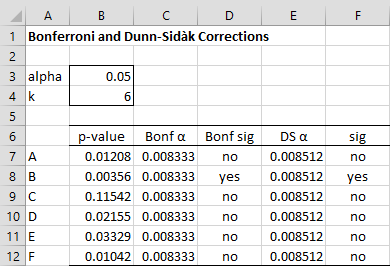
Example 1: Suppose that we have performed tests to determine the cancer risk of six environmental factors. The p-values of these tests are shown in Figure 1. Determine which of these factors are significant based on a familywise significance level of .05.
Figure 1 – Familywise significance
Based on the Bonferroni or Dunn-Sidàk correction factors, only environment factor B is significant (p-value = .00356 < .008333 or .008512 = corrected alpha) even though A, B, D, E, F would be significant if the correction factor were not taken into account.
These correction factors yield very conservative results, especially when there are a large number of hypotheses or when the hypotheses are correlated. This leads us to consider other approaches.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2018) Sidak correction
https://en.wikipedia.org/wiki/%C5%A0id%C3%A1k_correction
Wikipedia (2018) Bonferroni correction
https://en.wikipedia.org/wiki/Bonferroni_correction