Benjamini-Hochberg and Benjamini-Yekutieli Tests

Benjamini-Hochberg’s Test

For Benjamini-Hochberg’s adjustment, we again start with the largest p-value p_k (where  p₁ ≤ p₂≤ ^… ≤ p_k are the p-values of the multiple tests in ascending order) and identify the first i (staring from k) such that p_i < (i/k)α. Once this is found then tests 1, …, i are considered to be significant and the other tests are not significant.

Example 1: Repeat Example 1 of Dealing with Familywise Error using the Benjamini-Hochberg method.

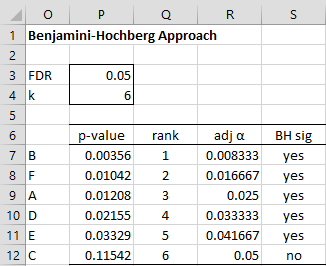
The result is shown in Figure 1. E.g. cell R8 contains the formula =P$3*Q8/P$4. The formulas in column S are identical to those used in column M of Figure 1 of Holm’s and Hochberg’s Tests.

Figure 1 – Benjamini-Hochberg test

Since the largest p-value for which p_i < (i/k)α is i = 5 (i.e. p₅ =.03329 < .041667), we conclude that all but test 6 (i.e. C) are significant.

This approach is more powerful than those considered previously; i.e. it accepts more risk of type I error in exchange for a lower type II error. This is appropriate when we have a large number of tests, especially when this is a filtering step for follow-up tests. In this case, we can accept a larger number of false positives since these will be removed in subsequent testing. This is often the case, for example, in genetic research.

Actually, in this approach, the alpha is considered to be a false discovery rate (FDR), reflecting the fact that we are willing to accept multiple type I errors (instead of trying to avoid even one type I error, as in the significance level). An FDR set at 5% means that we expect that 5% of the rejections of the null hypothesis will be wrong.

Finally note that in the Dunn-Sidàk version of the Benjamini-Hochberg test, we use the formula =1-(1-P$3)^(Q8/P$4) in cell R8.

Benjamini-Yekutieli’s Test

The Benjamini-Yekutieli approach is similar to the Benjamini-Hochberg approach, but instead of finding the test  j = max {i: p_i < (i/k)α}, we seek j = max {i: p_i < (i/k)α′} where α′ = α/. This test is more conservative than the Benjamini-Hochberg test.

Example 2: Repeat Example 1 of Dealing with Familywise Error using the Benjamini-Yekutieli method.

The approach shown in Figure 2 is identical to that for the Benjamini-Hochberg method shown in Figure 1, except that α =.05 is replaced by α′ = .02408 (cell V3) which can be calculated in Excel by the formula =0.05/SUMPRODUCT(1/W7:W12). This time, none of the environmental factors are found to be significant.

Figure 2 – Benjamini-Yekutieli test

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2018) False discovery rate
https://en.wikipedia.org/wiki/False_discovery_rate

Benjamini, Y. and Yekutieli, D. (2001) The control of the false discovery rate in multiple testing under dependency. Ann. Statist. 29(4): 1165-1188.
https://projecteuclid.org/journals/annals-of-statistics/volume-29/issue-4/The-control-of-the-false-discovery-rate-in-multiple-testing/10.1214/aos/1013699998.full

Benjamini, Y. and Hochberg, Y. (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. Roy. Statist. Soc. Ser. B 57 289–300
https://www.stat.purdue.edu/~doerge/BIOINFORM.D/FALL06/Benjamini%20and%20Y%20FDR.pdf