There are many versions of MI and so we will confine our remarks to the approach called the fully conditional specification (FCS) approach, also called the multivariate imputation by chained equations (MICE).
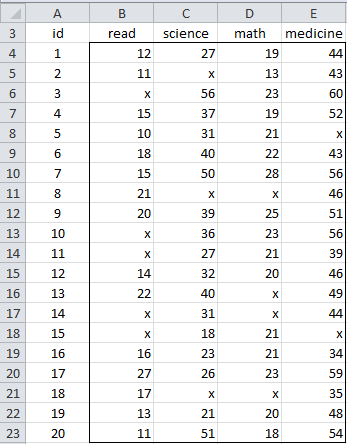
We will illustrate the FCS on several webpages using the data in Figure 1.
Figure 1 – Missing data example
Initialization
Before we can apply the FCS procedure we need to make sure that all the missing data is filled in (iteration 0). We can do this using any of the simple imputation approaches. Whatever limitations these approaches have will be overcome in subsequent iterations.
For each continuous variable with missing data find the mean x̄ and standard deviation s of non-missing data. Then pick a random value from the N(x̄, s2) distribution. As usual, this is done using the formula
=NORM.INV(RAND(), x̄, s)
For each categorical variable, say with d distinct values c1,…,cd. Find the proportion of the non-missing data elements in each category p1, …, pd. Then pick a random value from the corresponding multivariate distribution; i.e. the first h such that RAND() ≤ 
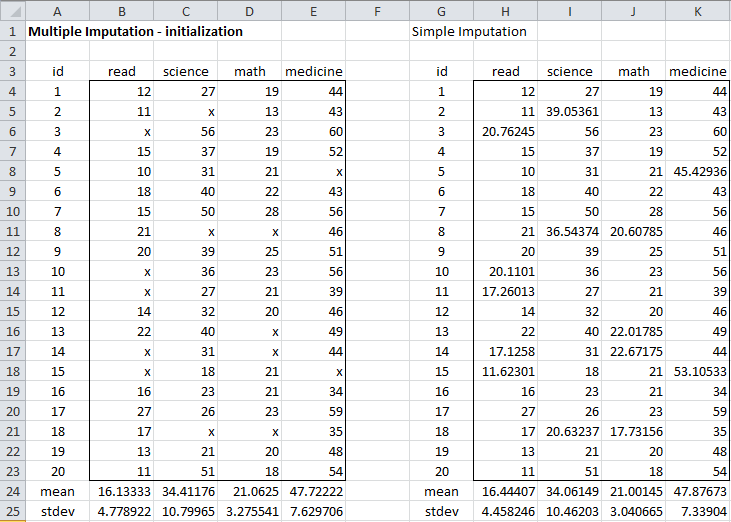
For the data in Figure 1, we can fill in all the missing data as shown in Figure 2. E.g. cell H6 contains the formula =NORM.INV(RAND(),B24,B25).
Figure 2 – Multiple imputation initialization
In Simple Imputation and Multiple Imputation Constraints we show how to generate the imputation shown in Figure 2 in Excel.
Iteration
For each successive iteration h > 0 we recalculate the originally missing values of variable xj using the complete values of
Continue the iterations until the maximum number of iterations is reached. This is usually 20-40 iterations (depending on the number of variables, since with a large number of variables this may take a long amount of time).
We illustrate one approach to these iterations in One Step of the FCS Procedure.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
UCLA (2021) How do I perform multiple imputation using predictive mean matching in R
https://stats.oarc.ucla.edu/r/faq/how-do-i-perform-multiple-imputation-using-predictive-mean-matching-in-r/
Murray, J. S. (2018) Multiple imputation: a review of practical and theoretical findings
https://projecteuclid.org/journals/statistical-science/volume-33/issue-2/Multiple-Imputation-A-Review-of-Practical-and-Theoretical-Findings/10.1214/18-STS644.full
Woods, A. D. et al. (2021) Missing data and multiple imputation decision tree. PsyArXiv
https://doi.org/10.31234/osf.io/mdw5r
Tufis, C. (2008) Multiple imputation as a solution to the missing data problem in social sciences
https://www.revistacalitateavietii.ro/journal/article/download/538/458/883