Rubin’s combination rules
If θ is one of the parameters we are interested in and the estimates of this parameter produced by the m imputations of the missing data are θ1, …, θm, with variances v1,…, vm, then the combined estimate of this parameter is
The within-imputation variance is then given by
and the between-imputation variance, which measures the uncertainty due to the imputation, is
The total variance is therefore
and so the standard error of the parameter is s = .
Note that the higher the value of m the lower the value of t. Note too that if there is no missing data then θ1=⋯= θm and so b = 0 and t = w.
Now define the relative increase in variance due to non-response r as follows:
![]() The test statistic for the null hypothesis θ = θ0 is
The test statistic for the null hypothesis θ = θ0 is
which has a t distribution with the following degrees of freedom
With small samples an improved estimate of df′ is as follows:
where n is the sample size (complete data). This improved version of df is always less than or equal to the previous version. In fact, if the first term in the denominator of df′ is replaced by 0 we get df.
As usual, the 1 – α confidence interval for the parameter θ is expressed as
where tcrit = T.INV.2T(α/2, df).
Assumptions
The combination rules described above assume that the estimates are asymptotically normally distributed, which may not always be the case.
For example, as observed in One Sample Hypothesis Testing for Correlation Coefficient, the correlation coefficient is not normally distributed. Fortunately, as was pointed out in that webpage the Fisher transform of the correlation coefficient is normally distributed, and so we can apply the combination rules to the Fisher transform and then take the inverse transform to get a combined value for the correlation coefficient.
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack furnishes the following array functions where R1 is a 2m × n array where the first m rows represent the values of m imputed population parameters (mean, coefficient, etc.), and the second m rows represent the corresponding standard errors for these parameters. The columns represent separate imputations. The argument size is the number of elements in the original sample (including missing data) and lab and head are as for DescStats (where lab defaults to FALSE and head defaults to TRUE).
ImputeVar(R1, size, lab, head) – outputs an array similar to range AE15:AO19 in Figure 4 summarizing the combination rules for variance.
ImputeParam(R1, size, lab, head, alpha) – outputs an array similar to range AE23:AL27 in Figure 4 based on the combination rules and the usual t-test using the stated value of alpha (default = .05).
Example
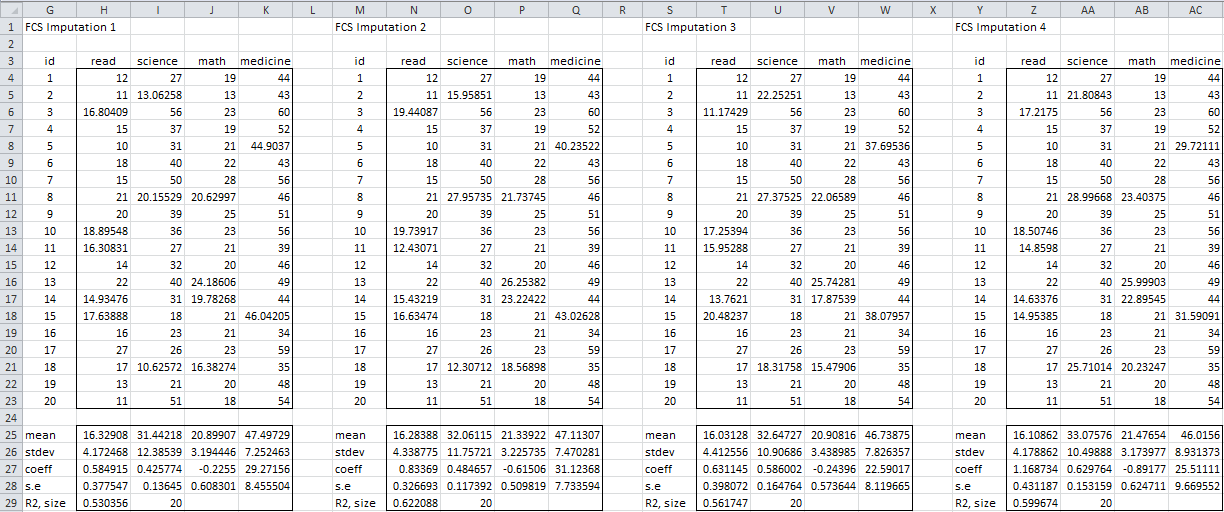
We illustrate these functions in the following figures. We begin by using ImputeFCS to generate 4 distinct imputations (see Figure 1) of the missing data in the example we have been using throughout this part of the website (see, for example, Figure 1 of Fully Conditional Specification). For each of these imputations, we use MISummary to create the compact summary described above (shown in rows 25 through 29 of Figure 1).
Figure 1 – Multiple imputations using FCS
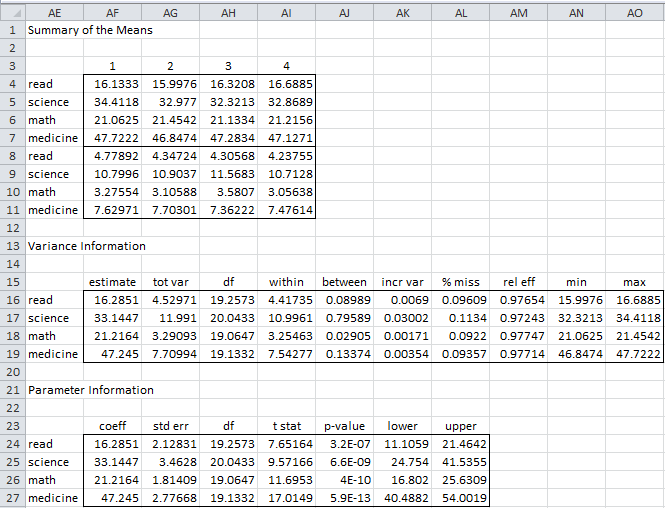
From this data, we manually create the range AE3:AI11 of Figure 2, which by way of illustration contains the means from the four imputations (in the first four rows and the standard deviations in the next four rows). The variance information (range AE15:AO19 of Figure 2) is then generated by the array formula
=ImputeVar(AE4:AI11,20,TRUE,TRUE)
The parameter information (range AE23:AL27 of Figure 2) is generated by the array formula
=ImputeParam(AE4:AI11,20,TRUE,TRUE)
Figure 2 – FCS summaries
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Links
References
Haymans, M. W., Eekhout, I (2019) Rubin’s rules. Applied missing data analysis with SPSS and (R) Studio
https://bookdown.org/mwheymans/bookmi/rubins-rules.html
UCLA (2021) How do I perform multiple imputation using predictive mean matching in R
https://stats.oarc.ucla.edu/r/faq/how-do-i-perform-multiple-imputation-using-predictive-mean-matching-in-r/
Murray, J. S. (2018) Multiple imputation: a review of practical and theoretical findings
https://projecteuclid.org/journals/statistical-science/volume-33/issue-2/Multiple-Imputation-A-Review-of-Practical-and-Theoretical-Findings/10.1214/18-STS644.full
Tufis, C. (2008) Multiple imputation as a solution to the missing data problem in social sciences
https://www.revistacalitateavietii.ro/journal/article/download/538/458/883
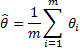
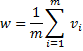
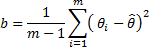
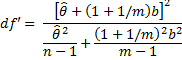
oh dear, I found that successfully. Pls ignore the message.
Are you able to send samples of these excel worksheets? I am working on combining pooled statistics from MI from output from SPSS and a template would be very helpful. Thanks!
You can download worksheets for all the examples on the website. See
https://www.real-statistics.com/free-download/real-statistics-examples-workbook/
Charles
Thanks for your reply. I also find the excel sheets useful but there were too many sheets stored in the link provided, would you mind telling me which file I should download for the excel table used above? Thanks.