FIML using Solver

Objective

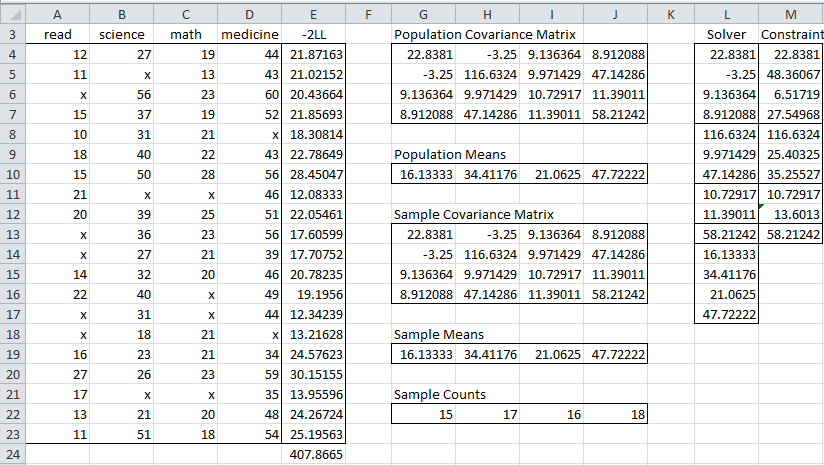
The goal of FIML is to find the values of the population parameters which minimize the value of -2LL. For the example we have been considering (Figure 2 of Initializing FIML, which is repeated here as Figure 1) cell E24 contains the value of -2LL.

Figure 1 – Initialization of FIML procedure

The current value has been set based on setting the population parameters, namely the covariance matrix and mean vector, equal to the sample values.

We show how to minimize the value in cell E24 by varying the population covariance and mean vectors using Excel’s Solver.

Solver Initialization

Since the population covariance matrix must be symmetric, we have some redundancy in its values (namely the upper triangle is completely determined by its lower triangle or vice versa). Thus we will look to vary the cells in the lower triangle of the population covariance matrix (e.g. via the formula =L10 in cell H7) and constrain the upper triangle (e.g. via the formula =H7 in cell J5). We, therefore, arrange the cells to be varied in the range L4:L17, where the first part consists of the non-redundant cells from the population covariance matrix followed by the cells from the mean vector.

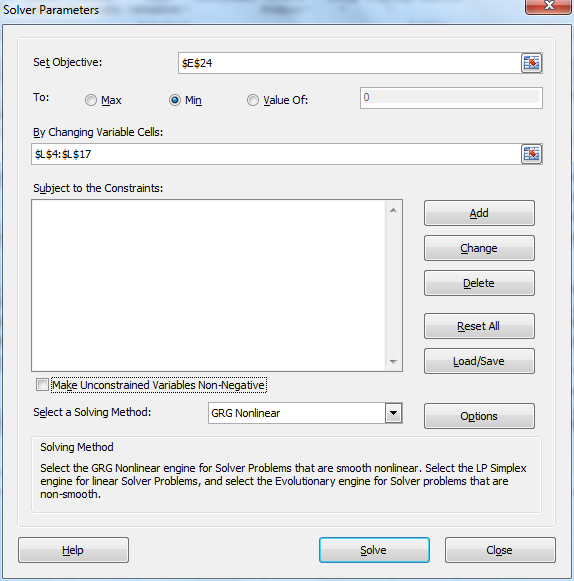
We next select Data > Analysis|Solver. When the Solver dialog box appears we fill in the values as described in Figure 2 and then click on the Solve button.

Figure 2 – Solver dialog box for FIML

It is important to choose Min and to uncheck the Make Unconstrained Variables Non-Negative.

Output from Solver

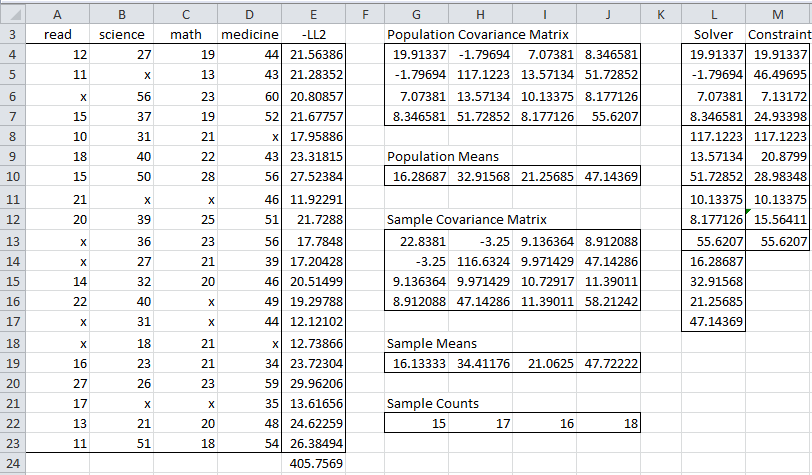
If everything goes well, Solver will find values for the population covariance matrix and mean vector which minimizes -2LL. This result is shown in Figure 3.

Figure 3 – FIML using Solver

Note that the value of -2LL (cell E24) went down from 407.8665 (in Figure 1) to 405.7569 after using Solver. The new values for the population covariance matrix and mean vector are shown in Figure 3 which can be compared with the sample values.

Constraints

We mentioned that the values in the population covariance matrix are constrained. There are additional constraints that we didn’t describe to Solver, but we could have if necessary. Click here for more information about adding these constraints to the Solver iteration.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Enders, C. K. (2001) The performance of the full information maximum likelihood estimator in multiple regression models with missing data. Educational and Psychological Measurement, Vol. 61 No. 5.
https://asu.elsevierpure.com/en/publications/the-performance-of-the-full-information-maximum-likelihood-estima

Allison, P. D. (2012) Handling missing data by maximum likelihood
https://statisticalhorizons.com/wp-content/uploads/MissingDataByML.pdf