We now explore another approach to dealing with missing data, based on the maximum likelihood function and used in logistic regression.
The basic premise is that instead of imputing the values of missing data, we try to estimate the value of some population parameter by determining the value that maximizes the likelihood function (actually the log of this function) based on the sample data that we have.
We assume that the data is missing at random (MAR) and has a multivariate normal distribution. If X represents all the data (including both x and y values) then the probability density function (pdf) is
Thus the likelihood function is given by
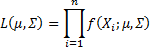where Xi is the ith row of X. The log-likelihood function is
where
Our goal is to maximize LL, which is the same as minimizing –2LL
where
But when there is missing data, we can’t calculate the population covariance matrix (or even the sample covariance matrix). Instead, we need to estimate it based on the data we have. In particular, we use the following alternative value:
where ki = the number of non-missing entries in the ith row of X and μi is the 1 × ki population mean vector μ with all the means corresponding to the missing entries in Xi removed, i.e. if μ = [μ(1) … μ(k)] then μi is μ with the elements μ(j) for which the data element xij is missing. Similarly, Σi is the ki × ki population covariance matrix Σ with the jth row and j column removed for all data elements xij in the ith row which are missing.
Our goal is to find the values for Σ and μ which maximize LL, or equivalently which minimize -2LL.
References
Enders, C. K. (2001) The performance of the full information maximum likelihood estimator in multiple regression models with missing data. Educational and Psychological Measurement, Vol. 61 No. 5.
https://asu.elsevierpure.com/en/publications/the-performance-of-the-full-information-maximum-likelihood-estima
Allison, P. D. (2012) Handling missing data by maximum likelihood
https://statisticalhorizons.com/wp-content/uploads/MissingDataByML.pdf
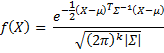
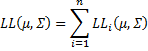
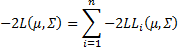
I would like to estimate a multinomial logit model (MNL) on a data set where my independent variables have missing data.
I do not what to exclude the data with missing values or use multiple imputation.
A little known statistical software called NLOGIT (or also known as LIMDEP), can implement such a model. This is how they describe it:
Instead of setting the missing value of the variable, x, to 0 and and maximizing the likelihood function, a search algorithm, excludes that x from the estimation procedure altogether and automatically assigns to it a parameter value of zero. The parameter estimate, θ, is then estimated solely on the sample population for which the variable was not excluded.
For example, if this was the formula for the MNL:
Uij=β1FASHij+β2QUALij+β3PRICEij+β4ASC4ij+εij
Suppose a row in the data set had a missing value for FASH, then the parameter would be set to 0, i.e. simply excluded from the formula in maximum likelihood estimation:
Uij=0FASHij+β2QUALij+β3PRICEij+β4ASC4ij+εij
Is this what FIML is doing?
Can I use the maximum likelihood function if my data has not a multivariate normal distribution?
Thanks
Bernardita,
The maximum likelihood function can be used with any distribution, but in the context off FIML we are assuming a multivariate normal distribution.
Charles