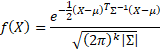Multivariate Normal Properties

Basic Concepts

Suppose that X = (x₁, …, x_k)^T is a k-tuple of random variables. X has a multivariate normal distribution N(µ, Σ) if the joint probability density function can be expressed as

Here Σ is the k × k population covariance matrix, µ = (µ₁, …, µ_k)^T is the population mean vector and |Σ| is the determinant of Σ. Note that the exponent of e consists of a scalar times the transpose of X – µ, the inverse of Σ and X – µ, which has dimension (1 × k) × (k × k) × (k × 1) = 1 × 1, i.e. a scalar. Thus, f(X) is a number.

If we partition X as

where X₁ is k₁ × 1 and X₂ is k₂ × 1 (and so k₁ + k₂ = k), then we can partition the mean and covariance matrix in a similar fashion

Here µ_i is k_i × 1 matrix and Σ_ij is a k_i × k_j matrix. We need to use the following two properties:

Properties

Property 1: X_i has a multivariate normal distribution N(µ_i, Σ_ii)

Property 2: A = X₂|X₁ has a multivariate normal distribution N(µ*, Σ*) with mean and covariance matrix

For a bivariate normal distribution

Thus

Relationship to EM algorithm

From the first equation, we have the estimate for a missing y in the E step, as described in EM Algorithm for Bivariate Normal Data.

If Z has a multivariate normal distribution N(μ, Σ) and we partition Z as

where X = k × 1 . Then we can partition the mean and covariance matrix as described previously

Here Σ_XX is a k × k matrix, Σ_Xy  is a k × 1 matrix, Σ_yX is a 1 × k matrix and Σ_yy is a scalar

Then A = y|X has a multivariate normal distribution with mean and covariance

Thus, we estimate the missing y value corresponding to X₀ (E step in the EM algorithm) by the formula

where

i.e. the sample means vector and covariance matrix (M step in the EM algorithm).

We show how this is done in EM Multivariate Normal Data with Missing Elements.

References

Wikipedia (2018) Multivariate normal distribution
https://en.wikipedia.org/wiki/Multivariate_normal_distribution