Likelihood Function and MLE
Definition 1: Suppose a random variable x has a probability density function f(x; θ) that depends on parameters θ = {θ1, θ2, …, θk}. For a sample {x1, x2, …, xn} the likelihood function is defined by
Here we treat x1, x2, …, xn as fixed. The maximum likelihood estimator (MLE) of θ is the value of θ that maximizes L(θ). We can then view the maximum likelihood estimator of θ as a function of the sample x1, x2, …, xn. We will commonly represent the maximum likelihood estimator of θ as θ-hat.
Ratio Test
Definition 2: Let θ-hat be the maximum likelihood estimator of θ for the sample {x1, x2, …, xn}. Suppose we want to test a null hypothesis regarding the parameters in θ and let θ’-hat be the maximum likelihood estimator of θ for the sample {x1, x2, …, xn} when the null hypothesis is true. Now define
λ can be viewed as a function of x1, x2, …, xn.. Clearly
and so 0 ≤ λ ≤ 1. For any given x1, x2, …, xn., values of λ near 1 correspond to the null hypothesis being true. The closer that λ is to 1 the more reasonable it is to accept the null hypothesis, while the farther away from 1 the more reasonable it is to reject the null hypothesis. Thus λ can be used as a statistic for testing the validity of the null hypothesis.
Suppose g(λ) is the probability density function for λ where g(λ) doesn’t depend on any unknown parameters, then for any significance level α, there is a value λ0 such that the cumulative distribution function F at λ0 takes the value α.
F(λ0) = Area0≤λ≤λ0 g(λ) = α
For those familiar with calculus, this is equivalent to
λ is the likelihood ratio test statistic for the hypothesis H0. We reject the null hypothesis if and only if the value of λ ≤ λ0 where λ is the value of the likelihood ratio for the sample {x1, x2, …, xn} and λ0 is the value such that F(λ0) = α.
References
Wikipedia (2012) Likelihood function
https://en.wikipedia.org/wiki/Likelihood_function
Wikipedia (2012) Likelihood ratio test
https://en.wikipedia.org/wiki/Likelihood-ratio_test
Wikipedia (2012) Maximum likelihood estimation
https://en.wikipedia.org/wiki/Maximum_likelihood_estimation
Hoel, P. (1962) Introduction to mathematical statistics, 3rd Ed. John Wiley and Sons
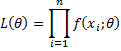
Question:
I am trying to identify acceptable variances based on historical data. For example, if I have week over week data for total time spent on social media, and when I receive next week’s data, I want to know if the time spent was unusually high, low, or average? How can I use excel to determine if the new week’s numbers fall within an acceptable range of times. And with that, how can I best determine what the acceptable range of times are?
Dan,
This does not seem like such a straightforward question. You need to decide on what criteria to use to determine an acceptable range of times. You might consider graphing the data and deciding on reasonable cutoff points. You might also consider using the results from other studies.
Charles
Dear Charles,
How to find Maximum Likelihood Estimates in Real Statistics XLS sheets. I tried searching thru Part-1A and Part1B but could not see MLE.
Thanks
Hello,
Examples can be found on the Goodness of Fit examples workbook, in association with the following webpage:
See https://real-statistics.com/distribution-fitting/distribution-fitting-via-maximum-likelihood/
Charles
I’m trying to use MLE to fit some historical time series data. I’m modeling changes in level as being dependent on the current level raised to some unknown exponent: dx(t) =x(t)^n.sigma.dW where x(t) is the level at time t, n is an unknown to be estimated, sigma is a scalar, and dW is a random process, assumed to be Gaussian. I set the whole thing up in Excel using dummy data to make sure it’s set up correctly first. But when I feed in the dummy data with n set to e.g. 0.5, I find the likelihood is maximized for very large values of n! Can I send you the sample sheet as I suspect I’m missing something obvious? Many thanks.
Rupert,
Yes, you can send me an Excel file with your data and analysis and I will try to give you some feedback.
Charles
Goodday Charles.
Please, how can I find log likelihood on my Excel worksheet
The Real Statistics add-in will show the log-likelihood for many functions and data analysis tools. Whether or not it is included depends on the specific test. This is explained in many places on the website (e.g. logistic regression).
Charles
Thanks for explaining the function. I have another question: What ist alpha? I don’t see an explanation of alpha anywhere. Could you please, please help me with that? Thank you in advance!!!
Joe
Joe,
Alpha is the significance level of the test, generally set to .05.
Charles
Oh, I see! Thank you! Sorry… I forgot.
Hi, pleas i need your help.
how i can drive the equation of Likelihood maximization.
and log likelihood maximization with respect the to the parameters THETA
Nejood,
See the following webpages for examples:
https://real-statistics.com/distribution-fitting/distribution-fitting-via-maximum-likelihood/
Charles
good evening, i have been following your work lately especially on the above subject matter.
Please i need your help as i need to calculate the maximum livelihood estimate for forest officers in my state.
Please let me if you will be chance so i can send the data to you to help me with the analysis.
Thanks
Daniel,
You can sends an Excel file with your data and analysis to me. Please clearly state what you are trying to accomplish. You can find my email address at Contact Us.
Charles
Question:
What is the reason for having a #value answer for the Max Likelihood part of the Chi-test?
Victor,
It is an error of some sort, but I would have to see the data to give you a more specific answer. If you send me an Excel file with your data, I could answer more specifically (my email address is available via Contact Us).
Charles