Property 3: The sample variance is an unbiased estimator of the population variance
Proof: If we repeatedly take a sample {x1,…,xn} of size n from a population with mean μ, then the variance s2 of the sample is a random variable defined by
it follows that
by Property 1 of Expectation we now have
By Property 2 of Estimators
Putting all the pieces together we get
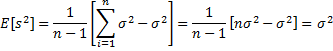 Reference
Reference
Wikipedia (2013) Variance
https://en.wikipedia.org/wiki/Variance#Sample_variance

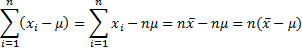
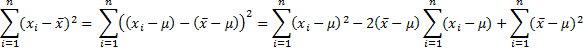
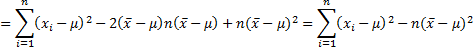
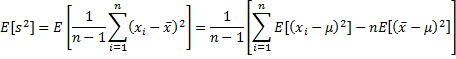
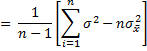
Dear Charles,
sorry, I’ve got another question…
I do not understand how do we formally move from the definition of the variance sigma^2 = E[(x-µ)^2] to the one you’re using i nthe demo sigma^2 = sum(E[(x_i – µ)^2]).
Thanks in advance,
Gilles
Dear Gilles,
What was written on the referenced webpage was a typing mistake: sigma^2 = E[(x-µ)^2] without the sum. I have now corrected this mistake on the webpage. Thanks for catching the error.
Charles