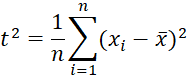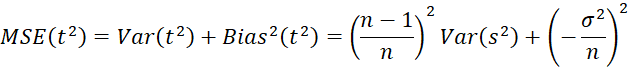Estimators

The following are desirable properties for statistics that estimate population parameters:

• Unbiased: on average the estimate should be equal to the population parameter, i.e. t is an unbiased estimator of the population parameter τ provided E[t] = τ.
• Consistent: the accuracy of the estimate should increase as the sample size increases
• Efficient: all things being equal we prefer an estimator with a smaller variance

Properties

Property 1: The sample mean is an unbiased estimator of the population mean

Proof: If we repeatedly take a random sample {x₁, x₂, …, x_n} of size n from a population with mean µ, then the sample mean can be considered to be a random variable defined by

Since each of the x_i is a random variable from the same population, E[x_i] = μ for each i, from which it follows by Property 1 of Expectation that:

Property 2: If we repeatedly take a sample {x₁, x₂, …, x_n}  of size n from a population with variance σ², then

Proof: Since the x_i are independent with variance σ², by Property 6.3b and 6.4b of Expectation

Small Populations

The proof of Property 2 depends on the sample members being selected (with replacement) independently of each other. This may not be the case where the sample is not a small fraction of the population. In this case, it can be shown that

where N = the size of the population.

Sample Variance

If we repeatedly take a sample {x₁, x₂, …, x_n} of size n from a population, then the variance s² of the sample (see Measures of Variability) is a random variable defined by

Property 3: The sample variance is an unbiased estimator of the population variance.

Click here for a proof of Property 3.

Biased and Unbiased Estimators

As stated above, t is an unbiased estimator of the population parameter τ provided E[t] = τ. We make the following definitions.

The bias of an estimator t of τ is Bias(t) = E[t] – τ. An estimator is unbiased if its bias is zero.

The mean squared error of the estimator is MSE(t) = E[(t–τ)²]. An estimator is efficient if this estimate has the smallest mean squared error.

Property 4: MSE = Var + Bias²

Proof: By Property 2 of Expectation

Var(t – τ) = E[(t – τ)²] – (E[t – τ])²

= E[(t – τ)²] – (E[t] – τ)² = MSE(t) – (Bias(t))²

Thus, an unbiased estimator is efficient if its mean square error is smaller than any other unbiased estimator.

Biased estimators

Property 5: The sample standard deviation s is a biased estimator of the population standard deviation σ. In fact, s has a negative bias.

Proof: By Property 3, the sample variance s² is an unbiased estimator of the population variance σ². By Property 2 of Expectation it then follows that

Var(s) = E[s²] – (E[s])² = σ² – (E[s])²

Assuming our sample has at least two elements, it follows that 0 < Var(s) = σ² – (E[s])², and so E[s] <  σ.

We note, without proof, that

Property 6:

By Property 6, Var(s²) → 0 as n → ∞. It follows that s² is a consistent estimator of σ².

Property 7: Define t² as

Then t² is a biased estimate of σ² with a negative bias.

Proof: Since t² = (n-1)s²/n, it follows that

We see that the bias is –σ²/n.

Observations: Note, though, that t² is asymptotically unbiased since E[t²] → σ² as n → ∞. Also note that

Since MSE(t²) → 0 as n → ∞, we conclude that t² is a consistent estimator of σ².

References

Wikipedia (2012) Estimator 
https://en.wikipedia.org/wiki/Estimator

Howell, D. C. (2010) Statistical methods for psychology (7^th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf

Wikipedia (2022) Bias of an estimator
https://en.wikipedia.org/wiki/Bias_of_an_estimator

Vaia (2024) Estimator bias
https://www.vaia.com/en-us/explanations/math/statistics/estimator-bias/