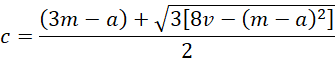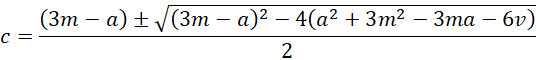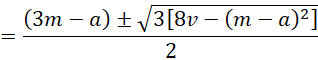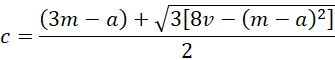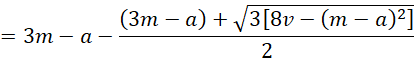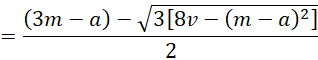Triangular Dist MoM Fit Detail | Real Statistics Using Excel

Property 1: If you know the value of a then you can estimate b and c by

b = 3m – a – c

Proof: As shown in Method of Moments: Triangular Distribution, the mean m and variance v of a triangular distribution follow the following equations

m = (a + b + c)/3

v = (a² + b² + c² – ab – ac – bc)/18

From the first equation, it follows that

b = 3m – a – c

b² = (3m – a – c)² = 9m² + a² + c² – 6ma – 6mc + 2ac

From the equation for the variance, it follows that

18v = a² + b² + c² – ab – ac – bc

Substituting the expressions for b and b², it follows that

18v = a² + 9m² + a² + c²– 6ma – 6mc + 2ac + c² – ab – ac – bc + c² – 3ma + a² + ac – ac – 3mc + ac + c²

= 3a² + 9m² +3c² – 9ma – 9mc + 3ac

This results in one equation in one unknown

6v = a² + 3m² +c² – 3ma – 3mc + ac

which is equivalent to

c² + (a – 3m)c + (a² + 3m² – 3ma – 6v) = 0

Using the quadratic formula, it follows that

Actually, we can use the version with the positive sign before the square root symbol.

This has a solution provided 8v ≥ (m – a)².

Observation: Note that

b = 3m – a – c

and so b can also be calculated via the formula for c above except that the negative sign is used before the square root symbol.

References