Using Iterative Search
We can estimate the parameter values of a triangular distribution that fits the data in a data set by iterative search. We won’t go into all the details of how to do this, but instead, explain the TRIANG_FITM that implements this approach.
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet function that estimates the parameters of a triangular distribution that fits the data in R1 based on the method of moments.
TRIANG_FITM(R1, lab, lo, hi, iter, exta, extb, iterb, iterc): returns a column array with the estimated values of the parameters a, b, c; along with the mean, variance, and skewness based on the data in R1 as well as based on the distribution parameters; and finally the MLE and the sum of squares.
The arguments are exactly as for TRIANG_FIT (see Fitting a Triangular Distribution via MLE), except there is also an iterb parameter. For every combination of a and c, as described in Fitting a Triangular Distribution via MLE, the function tests the values b1, b2, …, bm as potential values for b (for these a and c) where m = iterb – 1, and
bi = a + i(c–a)/iterb
Iterative Search Example
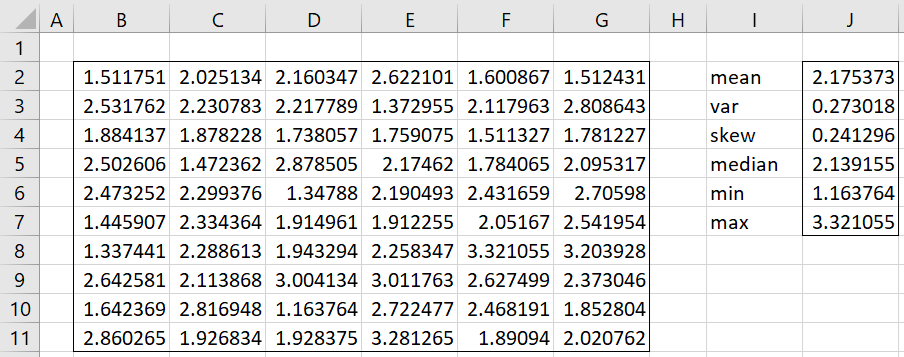
Example 1: Repeat Example 3 of Method of Moments: Triangular Distribution using the TRIANG_FITM function. The data is repeated in Figure 1.
Figure 1 – Fitting data to a triangular distribution
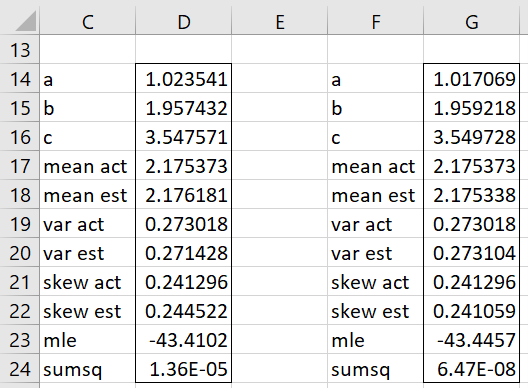
We use the formula =TRIANG_FITM(B2:G11,TRUE) to obtain the results shown in range C13:D24 of Figure 2. These values are similar to, but not exactly the same as, the values in Figure 5 of Method of Moments: Triangular Distribution. Note that the sum of squares (cell D14 in Figure 2) is not quite as good as the equivalent value in Figure 5 of Method of Moments: Triangular Distribution, but the MLE (cell D23) is a little better.
Figure 2 – Using TRIANG_FITM
Finally, we increase the value of iter to 250, hoping to get a lower sumsq value. This is done by inserting the formula =TRIANG_FITM(B2:G11,TRUE,,,250) in the range F14:G24. We see from Figure 2 that we do indeed get more accurate mean, variance, and skewness values, but at the cost of a lower MLE (as well as a slower run time).
We can also improve the accuracy by reducing the exta and extc arguments as described in Fitting a Triangular Distribution via MLE.
Solving equations approach
TRIANG_FITM also supports the approach described at the beginning of Method of Moments: Triangular Distribution based on solving equations.
Real Statistics Function: We can use the equation-solving approach in TRIANG_FITM when a or c is known. In this case, you just need to set the a or c argument to the known value and set iter = 0. If both a and b are known and you want to use the mean to estimate b then set iter = 0, but if you want to use the median to estimate b then set iter = -1.
Examples when iter = 0 or -1
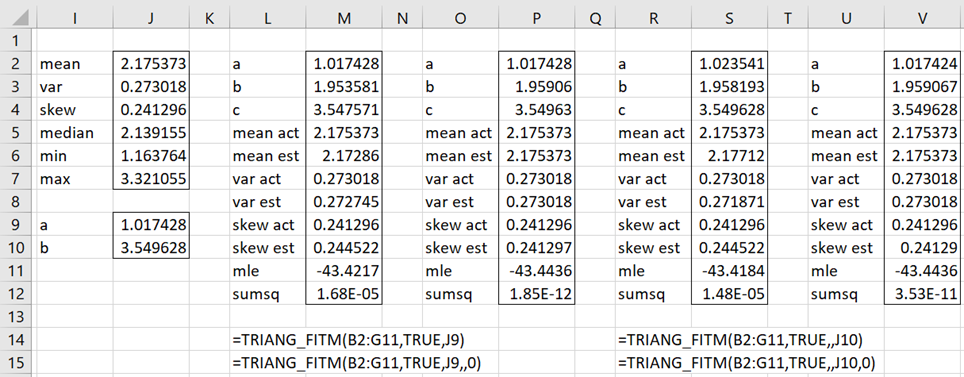
Example 2: Repeat Example 2 of Method of Moments: Triangular Distribution using TRIANG_FITM. We need to (a) fit the data in range B2:G11 of Figure 1 to a triangular distribution using the method of moments when we know that a = 1.017428 and (b) fit the data if, instead, we know that c = 3.549628.
The results are shown in Figure 3. Range L2:M12 contain the results for (a) using the 3-parameter algorithm, while O2:P12 contains the results using the 2-parameter algorithm. Range R2:S12 contain the results for (b) using the 3-parameter algorithm, while U2:V12 contains the results using the 2-parameter algorithm.
Figure 3 – TRIANG_FITM when a or c is known
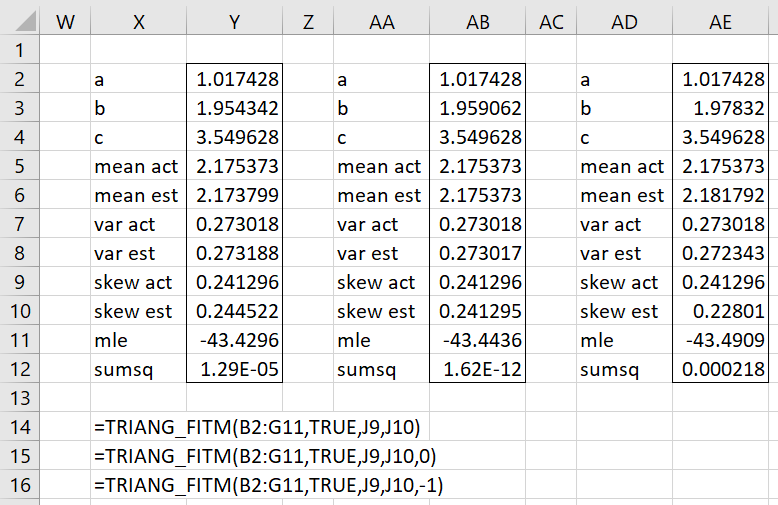
Example 3: Repeat Example 1 Method of Moments: Triangular Distribution using TRIANG_FITM. This time, we want to fit the data in Figure 1 to a triangular distribution when we know that a = 1.017428 and c = 3.549628.
Figure 4 shows three approaches for estimating b when a and c are known. Range X2:Y12 contain the results using the 3-parameter algorithm, while AA2:AB12 contains the results using the 1-parameter algorithm based on the mean and range AD2:AD12 contain the results using the 1-parameter algorithm based on the median.
Figure 4 – TRIANG_FITM when a and c are known
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Cook, J. (2015) Fitting a triangular distribution
https://www.johndcook.com/blog/2015/03/24/fitting-a-triangular-distribution/#:~:text=One%20way%20to%20fit%20a,if%20these%20values%20are%20known.
Kotz, S., van Dorp, R.(2004) The triangular distribution. Beyond Beta
https://books.google.it/books/about/Beyond_Beta_Other_Continuous_Families_Of.html?id=JO7ICgAAQBAJ&redir_esc=y