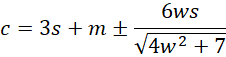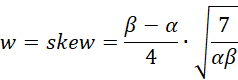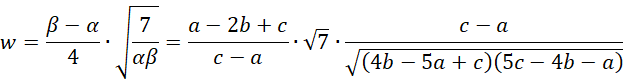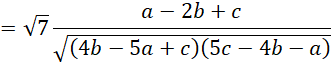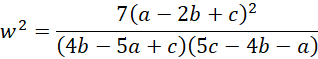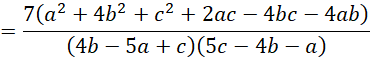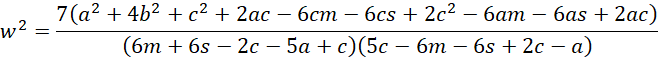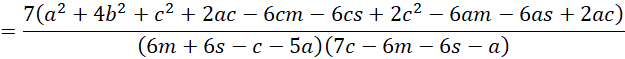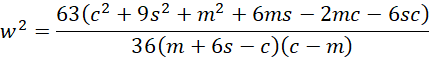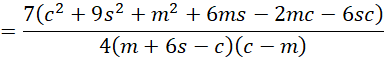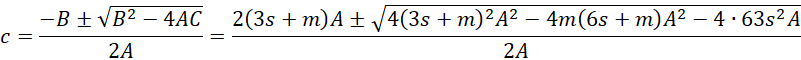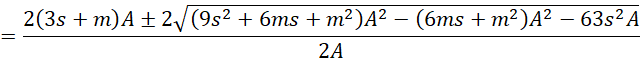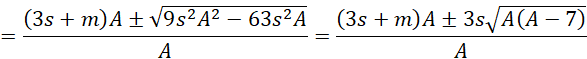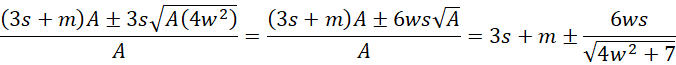Property 1: If a data set X follows a PERT distribution, we can estimate the distribution parameters a, b, and c by setting the formulas for the distribution mean, standard deviation, and skewness to the corresponding sample values m, s, and w. In particular
Proof: First, we observe that the skewness of the data in X (see PERT Distribution).
where
Note that
Thus
It now follows that
As we observed in Method of Moments: PERT Distribution
Hence
Also
Thus, the numerator of the expression for w2 is equal to
We also know from Method of Moments: PERT Distribution that a = c – 6s and so a2 = c2 -12cs + 36s. Thus, the numerator of the formula for w2 is equivalent to
We also observe that the denominator of the formula for w2 is equivalent to
Putting the pieces together, we see that
We now solve for c.
This is equivalent to the quadratic equation
where
In fact, if we also define
then, the original equation can be expressed as
Using the quadratic formula, we get
which completes the proof.
References
Rao, K. S., Viswam, N., Anjaneyulu, G. (2021) Estimation of parameters of Pert distribution by using method of moments
https://www.ijraset.com/fileserve?FID=38239
Wikipedia (2023) PERT distribution
https://en.wikipedia.org/wiki/PERT_distribution