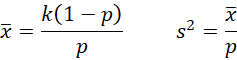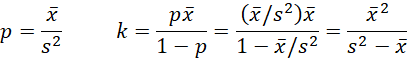Given a collection of data that may fit the negative binomial distribution, we would like to estimate the parameters which best fit the data. We illustrate the method of moments approach on this webpage. Click here to see another approach, using the maximum likelihood method.
Parameter estimates
As shown in Negative Binomial Distribution, we can estimate the sample mean and variance for the negative binomial distribution by the population mean and variance, as follows:
Solving for k and p, we get
We also see that
Log-likelihood function
The likelihood function for the negative binomial distribution is
It follows that the log-likelihood function is
Example
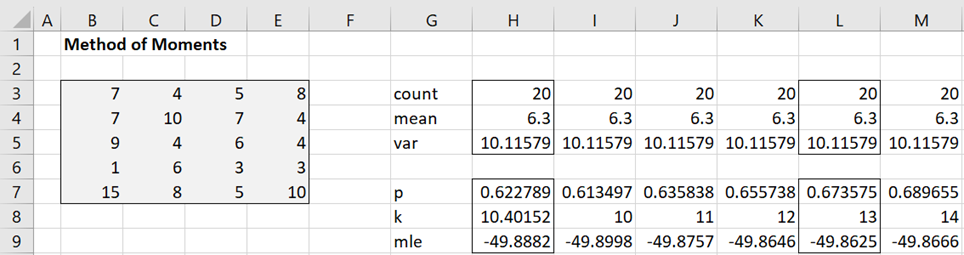
Example 1: Use the method of moments to find the parameters of the negative binomial distribution that best fits the data in Figure 1.
Figure 1 – Method of Moments example
We see from column H that p = .622789 and k = 10.40152. If we require that k be an integer, then we see that k = 11 is better than k = 10 (i.e. higher MLE). Actually, we see from column L that k = 13 and p = .673575 achieve a higher value for LL.
Note that the formula in cell H9 is
=SUMPRODUCT(GAMMALN($B3:$E7+H8))-SUMPRODUCT(LN(FACT($B3:$E7)))-H3*GAMMALN(H8)+H3*H8*LN(H7)+LN(1-H7)*SUM($B3:$E7)
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Wikipedia (2023) Negative binomial distribution
https://en.wikipedia.org/wiki/Negative_binomial_distribution