Basic Concepts
From Lognormal Distribution, we know that
Thus
and so
from which it follows that
and so
or
Since
it follows that
and so
which gives us the estimates for μ and σ based on the method of moments.
Example
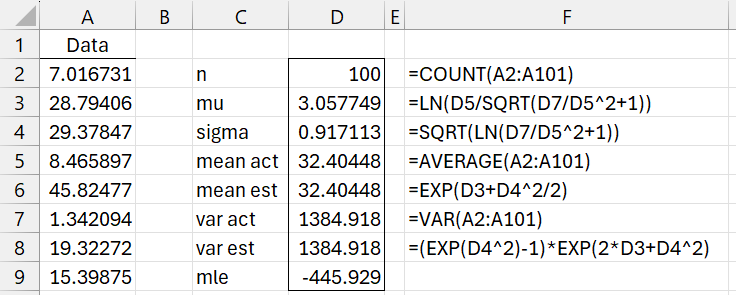
Example 1: Estimate the mu and sigma parameters for the log-normal distribution that fits the sample of size 100 in column A of Figure 1 (only the first 8 elements are displayed) using the method of moments.
Figure 1 – Fitting a lognormal distribution
The formula for the log-likelihood function (cell D9) is
=-D2*(LN(2*PI())/2+LN(D4)+(D3/D4)^2/2)+(D3/D4^2-1)*SUM(LN(A2:A101))-SUMSQ(LN(A2:A101))/(2*D4^2)
This formula is derived in Fitting Lognormal Parameters via MLE.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Genos, B. F. (2009) Parameter estimation for the Lognormal distribution
https://scholarsarchive.byu.edu/cgi/viewcontent.cgi?article=2927&context=etd
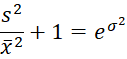
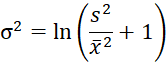
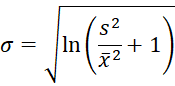
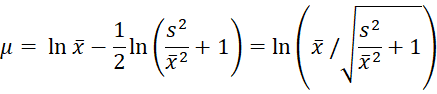
Dear Charles,
When I apply the formula =LOGNORM_FIT(A2:A101;1) in the Excel workbook Example1, I get the same results as in the example above, except for the parameter mle = 176.884. Additionally, when using the formula =LOGNORM_FIT(A2:A101;1;1), I get mle = 179.952.
I obtain the same result for mle using the Distribution Fitting Tool, and I am utilizing the latest version of XRealStats.xlam (Release 9.3).
Is there a different formula for the mle parameter applied in the LOGNORM_FIT function compared to the formula for the log-likelihood function (cell D9)? If so, which formula is it?
I have an additional question: In the example “Fitting Lognormal Distribution via MLE,” it was shown that the MLE method gives a better result for mle = -443.502 and -443.504 compared to the “Method of Moments” mle = -445.929 (less negative mle is better?). Is this always the case? If so, shouldn’t the MLE method be the default for the LOGNORM_FIT function instead of the MoM method, and the generally preferred method?
Many thanks for your website. I find it the best resource on the Internet for this topic!
Hello Davor,
1. I also found an error in the MLE calculation for LOGNORM_FIT — a week or two ago. I have already made the correction in the software and am planning to release this correction in the next software release, Rel 9.4. I hope to have this release ready within 1 or 2 weeks.
In any case, thank you for informing me of the error. I don’t always catch these error, and so I am grateful to you and people like you that catch these errors.
2. By definition, the MLE fit should never yield an log-likelihood estimate (LL) value worse than the MoM fit. Sometimes the LL value for the MoM fit is almost as good as the MLE fit, but the moments (mean and variance) for the MoM fit are sufficiently better than those produced by the MLE fit that you might find the MoM fit more useful.
Charles