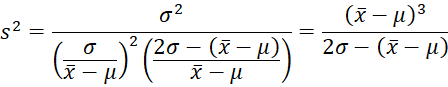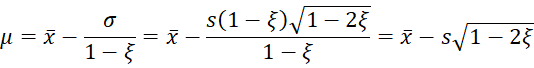Basic Approach
Suppose that the location parameter μ is known and we are able to calculate the mean and variance of a sample that we suspect may be from a population that follows a Generalized Pareto (GPD) distribution. We show how to estimate the other two parameters using the method of moments, as follows.
Estimates if μ is known
Since
solving for ξ, we obtain
It now follows that
We also know that
Thus
Solving for σ, we get
Thus
which provides us with the estimates for σ and ξ if μ is known. In summary, we have the following property.
Property 1: The following formulas provide estimates for the GPD parameters σ and ξ if μ is known.
Estimates if μ is unknown
If μ is not known, then let γ = the skewness of the sample data. Then for ξ < 1/3 (and so 1–3ξ > 0), we know that
Then
The roots of this equation can be obtained using Bairstow’s method. You can use any real root ξ < 1/3.
Since
it follows that
Finally, since
it follows that
Example
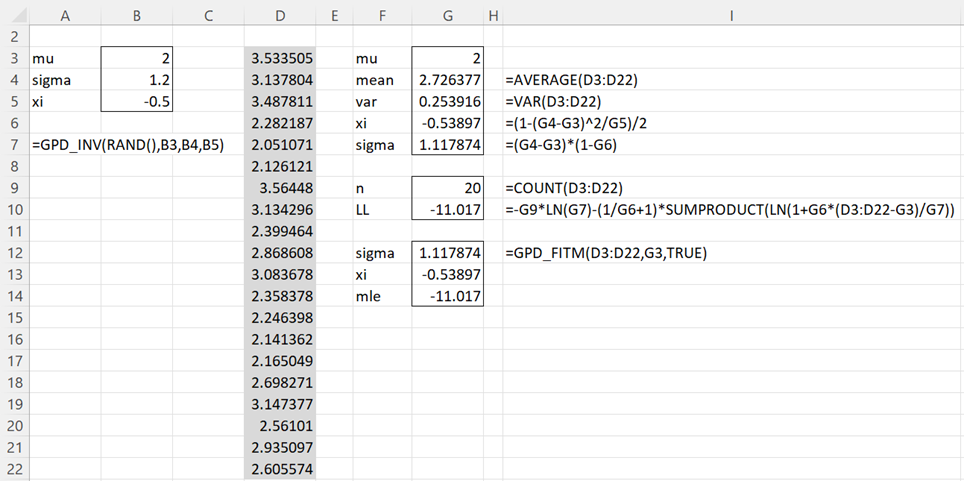
Example 1: Using the method of moments, estimate the values of the σ and ξ parameters for the GPD that best fits the data in column D of Figure 1 assuming that the location parameter μ = 2.
Figure 1 – Fitting data to a GPD
Cells G6 and G7 of the figure show the estimates of the shape and scale parameters using Property 1.
Note that the data in column D was created by inserting the formula =GPD_INV(B3,B4,B5) in cells D3 through D22. The resulting estimates of σ = 1.117874 and ξ = -0.53897 in cells G7 and G6 are pretty close to the population parameters σ = 1.12 and ξ = -0.5 shown in cells G7 and G6.
Log-likelihood
For a sample x1, …, xn that follows a Generalized Pareto distribution the likelihood function is
which results in the log-likelihood function
This is how the formula in cell G10 (and displayed in I10) was obtained.
Examples Workbook
Click here to download the Excel workbook with the example described on this webpage.
References
Mathworks (2022) Generalized Pareto distribution
https://www.mathworks.com/help///stats/gpcdf.html
Wikipedia (2022) Generalized Pareto distribution
https://en.wikipedia.org/wiki/Generalized_Pareto_distribution
Chu, J., Dickin, O., & Nadarajah, S. (2019). A review of goodness of fit tests for Pareto distributions. Journal of Computational and Applied Mathematics, 361, 13-41. https://doi.org/10.1016/j.cam.2019.04.018