Given a collection of data that may fit the exponential distribution, we would like to estimate the parameter that best fits the data. We illustrate the method of moments approach on this webpage. We show another approach, using the maximum likelihood method in Fitting an Exponential Distribution via MLE.
Example
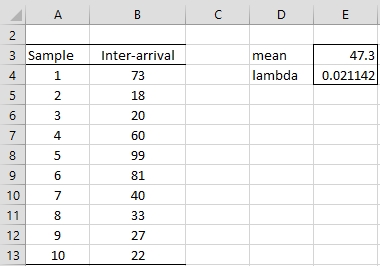
Example 1: Suppose the inter-arrival times for 10 people waiting for service at a supermarket checkout are as shown in range B4:B13 of Figure 1. Assuming a Poisson process, find the distribution that fits the data.
Figure 1 – Fitting an exponential distribution
As described in Exponential Distribution, inter-arrival times in this case follow an exponential distribution, and so we need to estimate the value of the lambda parameter. But we know that the (population) mean of an exponential distribution is the reciprocal of the lambda parameter, and so we can estimate the lambda parameter as the reciprocal of the sample mean.
The result is shown in cell E4 using the formula =1/E3.
Many of the distributions we describe on this website can be handled as for the exponential distribution described above. For example, the parameters for the normal distribution can be estimated by the sample mean and standard deviation. Similarly, the lambda parameter for the Poisson distribution can be estimated by the sample mean. Also, the gamma distribution parameters can be calculated as β = s2/x̄ and α = x̄/β.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Wikipedia (2017) Exponential distribution
https://en.wikipedia.org/wiki/Exponential_distribution
The survival time (in years) of a H.I.V. positive person after taking ARV drugs can be modeled by an exponential distribution with parameter l. Given a sample token from this distribution, use the method of moments to determine an estimator for the parameter
What is your question?
Charles