Basic Concepts
Given a collection of data that we believe fits a particular distribution, we would like to estimate the parameters that best fit the data. We now describe one method for doing this, the method of moments. Elsewhere we will describe two other such methods: maximum likelihood method and regression.
In the method of moments approach, we use facts about the relationship between distribution parameters of interest and related statistics that can be estimated from a sample (especially the mean and variance). We will use the sample mean x̄ as our estimator for the population mean μ and the statistic t2 defined by
as an estimator for the population variance σ2. x̄ and t2 are implemented in Excel via the AVERAGE and VAR.P functions, respectively.
Sample vs. Population Variance
From Estimators, we know that t2 is a biased estimator, but as the sample size gets larger, t2 becomes (asymptotically) unbiased and consistent.
Since often our samples are small, we will tend to use the sample variance s2, which is an unbiased, consistent estimator, instead of σ2. This is not technically the method of moments approach, but it will often serve our purposes. s2 is implemented in Excel via the VAR.S function. Note too that when we use s2 in the following examples, we should technically replace s2 by (n–1)s2/n to get t2.
Topics
- Exponential Distribution
- Weibull Distribution
- Beta Distribution
- Pareto Distribution
- Uniform Distribution
- Triangular Distribution
- PERT Distribution
- Lognormal Distribution
- Generalized Extreme Value (GEV) Distribution
- Generalized Pareto Distribution (GPD)
- The Generalized Gamma Distribution
- Real Statistics Support
Other Distributions
Many of the distributions we have studied on this website can be handled as for the exponential distribution described above. For example, the parameters for the normal distribution can be estimated by the sample mean and standard deviation. Similarly, the lambda parameter for the Poisson distribution can be estimated by the sample mean.
The gamma distribution parameters can be calculated as β = s2/x̄ and α = x̄/β.
The geometric distribution parameter can be estimated as p = 1/(1+x̄).
We can estimate the Gumbel distribution parameters by β = s√6/π and μ = x̄ – βγ where γ is the Euler-Mascheroni constant with a value approximately equal to .577215665 (see Gumbel Distribution).
The Logistic distribution parameters are estimated by μ = x̄ and β = s√3/π.
The Laplace distribution parameters can be estimated by μ = x̄ and β = s/√2.
Since the mean and standard deviation of the Cauchy distribution are undefined, these cannot be used to estimate the distribution’s parameters. A related approach is to estimate the µ parameter by the median and the σ parameter by half the interquartile range of the sample. A better estimate for µ is the mean of the middle 24% of the sample; i.e. =TRIMMEAN(R1,.76) where R1 contains the sample values.
Reference
Wikipedia (2021) Method of moments (statistics)
https://en.wikipedia.org/wiki/Method_of_moments_(statistics)
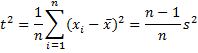
Dear Charles
I have one question. Given that i have mean and SE, whats the proper way to find parameters of a beta distribution?
Best Regards
Hello,
Use the approach described at
https://real-statistics.com/distribution-fitting/method-of-moments/method-of-moments-beta-distribution/
Charles
Hi Charles,
I think there is a typo in the estimation of beta for Gumbel distribution:
Beta=s*sqrt(6)/Pi
Many thanks for your website, it is very useful!
Thank you very much for identifying this error. I have now made the correction.
I appreciate your help in improving the accuracy of the website.
Charles