Weibull with Censored Data

Basic Concepts

In estimating the parameters of a Weibull distribution in Fitting Weibull Parameters via MLE, there was complete data. This isn’t always the case, as we shall see from the following example. Suppose we run a test on twenty components whose time to failure follows a Weibull distribution. Suppose too that at the end of the test period five of the components have not yet failed. This is what is called (right) censored data. Consequently, we don’t know the time to failure of these five components, but we do know that the time to failure is some positive value.

In such cases, we use the following modified version of the likelihood function where f(x) is the pdf and F(x) is the cdf of a distribution. We assume that n components fail by time t, while m components have not yet failed.

Likelihood function censored Weibull

Our goal is to maximize the log-likelihood function

Log-likelihood Weibull censored data

For the Weibull distribution

ThusLL Weibull censored data

Step-by-step Method

We can use Solver to find the values of α and β that maximize LL(α,β). Alternatively, we can use Newton’s method based on the extension to the iterative approach described in Fitting Weibull Parameters via MLE and Newton’s Method where there is no censored data.

Step 0: make an initial guess β0 for the value of β.

Step k+1: Assuming that we have an estimate  of βk, we define a new estimate βk+1, that should be more accurate, as follows:

Iteration of beta

where

and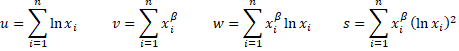

This process is repeated until the value of βk converges, at which point we calculate alpha by

Formula for alpha

Convergence occurs when h(βk) is close to zero or βk+1 ≈ βk.

Examples

Example 1: Estimate the parameters for the Weibull distribution that best fits the data in Example 1 of Fitting Weibull Parameters via MLE where in addition two other components have not failed after 900 hours.

The results are shown in Figure 1, which implements the iterative method described above with convergence occurring after about 6 iterations.

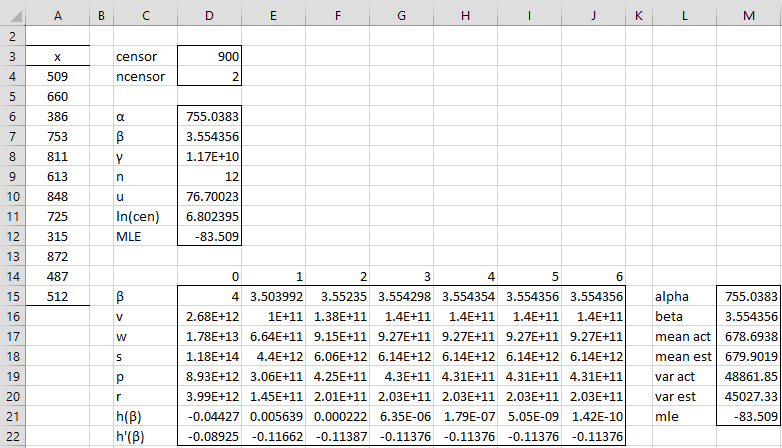
Weibull parameters censored data

Figure 1 – Estimating Weibull parameters for censored data

The formulas in the figure are as shown in Figure 2 of Fitting Weibull Parameters via MLE and Newton’s Method with the following changes:

Cell Item Formula
D6,M15   =(J20/D9)^(1/D7)
D11 ln(censor) =LN(D3)
D12,M21 MLE =D9*(LN(D7)-D7*LN(D6))+(D7-1)*D10-SUMPRODUCT((A4:A15/D6)^D7)-D4*(D3/D6)^D7
E19   =$D$4*$D$3^E15*$D$11
E20   =$D$4*$D$3^E15+E16
M17 actual mean =(SUM(A4:A15)+D4*(D3+WEIBULL_MRL(D3,D6,D7)))/(D9+D4)
M19 actual variance =WEIBULL_CVAR(A4:A15,D6,D7,D3,D4)

Figure 2 – Key formulas in Figure 1

We know the time to failure of 12 elements, but not of the two elements that have not failed yet. But, we can estimate the time to failure of these two censored elements (e.g. by using WEIBULL_MRL function as described in Survivability and the Weibull Distribution). These estimates depend on the alpha and beta parameters. We can estimate the mean and variance of all the data by using the following functions.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following functions.

WEIBULL_CMEAN(R1, alpha, beta, ncensor, censor) = the mean of the data in the column range R1 combined with the mean time to failure of ncensor data elements that have not yet failed at time censor, with this estimate based on the Weibull distribution with parameters alpha and beta.

WEIBULL_CVAR(R1, alpha, beta, ncensor, censor, iter) = the variance of the data in the column range R1 combined with the variance of the failure times of the ncensor data elements that have not yet failed at time censor, with this estimate based on iter simulations (default 20,000) from a Weibull distribution with parameters alpha and beta.

There is also the following Real Statistics array function where

WEIBULL_FIT(R1, lab, iter, bguess, ncensor, censor, viter):  returns an array with the Weibull distribution parameter values alpha and beta, actual and estimated means and variances, and MLE based on the data in the column range R1 combined with the estimated mean time to failure of ncensor data elements that have not yet failed at time censor (at which time no more failures are recorded). If ncensor = 0 (default) then no censoring occurs and the censor and viter arguments are ignored.

If lab = TRUE (default FALSE) a column of labels is appended to the output. iter = the maximum number of iterations using Newton’s method (default 20) based on an initial guess for the beta parameter of bguess (if omitted an internal algorithm generates an initial guess).

Example Continued

We can calculate the actual mean and variance using the WEIBULL_CMEAN and WEIBULL_CVAR functions. We can calculate the mean and variance based on the estimated alpha and beta parameters. If viter > 0 then the actual variance is estimated using simulation via the WEIBULL_CVAR function. If viter = 0 (default) then this value is not calculated (especially since the simulation may take a fair amount of time to return a reasonable value).

We can calculate the value in cell M17 of Figure 1 using the formula

=WEIBULL_CMEAN(A4:A15,D6,D7,D3,D4)

We can also calculate the values in range L15:M21 using the array formula

=WEIBULL_FIT(A4:A15,TRUE,,4,2,900,20000)

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

EpiX Analytics (2018) Using optimization to maximize a likelihood calculate to obtain MLEs
https://modelassist.epixanalytics.com/display/EA/Using+optimization+to+maximize+a+likelihood+calculation+to+obtain+MLEs

18 thoughts on “Weibull with Censored Data”

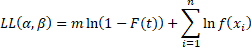
  1. Charles
    how to handle Censored sample having different value, in this case you have two parts censored both at 900 but if I would have at example Parts censored at 700, 950,850,900

    Reply

  2. Hi Charles,
    Thank you very much for your web pages, which are very helpful.
    Are left censored data supposed to be treated the same way as right censored data (eg, in your equation for L and LL)?
    If differently, should then the left censored data be included in another multiplicative factor F(x)^k to your L for k left-censored-data-points? If they are treated in the same way, then your m will become m+k, correct?
    Thank you very much in advance,
    -gk

    Reply

  3. Hi Charles,
    If I have another set of K data points that do not have their starting times but do have their failed times (so call left censored data), would it be plausible to multiply an additional term F(x)^k to your LL function above and then proceed to find the alpha and beta maximizing the LL?
    If yes, what else do I need in the solving process in addition to what you have given above?
    Many thanks in advance!
    GK

    Reply

  4. Hi Charles,
    I have a very basic question. What is a censor? Is it merely a parameter that filters out data that you do not want to include in the analysis because a failure has not yet occured?
    Cheers,
    Henry

    Reply

    • Hi Henry,
      I know what censored data is, but I have not heard of a parameter called a censor. In any case, as you have said, censored data represents data that has not yet failed.
      Charles

      Reply

  5. Hi,
    For value p=mt^beta lnt, I don’t know the value m and t coming from.
    is the m value is the slope, which equal to 1/beta and t is X variable. Please explain.
    THank you
    thu

    Reply

  6. Dear Charles,
    Before I start to explain my problem, I would like to make a big compliment to your website first. It really helps to bring complex statistical issues into practice, and especially in Excel. Your instructions for formulas and add-on are clear and comprehensive.

    At the moment I am stuck with estimating Weibull parameters using (Newton’s method) with censored data. I copied the data and formulas from the website. Play around with it to get it work and for better understanding before I transpose the examples to my project (8 sets of right censored reliability data each 50 samples, running 1000 cycles).

    So, I started with Fitting Weibull Parameters using MLE and Newton’s Method (no censored data) which works fine. I copied this calculation as the basis for Fitting Weibull parameters using Newton’s method (with censored data). Then I moved cells down to add ‘censor’ and ‘ncensor’ fields, add before columns H, 2 extra columns for 2 iterations to keep the cell reference D7, M16 to J15 intact, add blank cells C19,J20 for the formulas E19 and E20 as in the instruction and copied them over the range D19: J20.

    After I entered the changed formulas from the instruction and pressed F9 (calc.) I see the following results in ‘Censor’ D3: 760.9381, Beta D7, M16: 4.141938 and after 4 iterations H(beta) returns zero. Not after the expected 6. Further act mean returns ‘_VALUE’ and formula WEIBULL_FIT(A4:A15, TRUE , , 4, 2, 900, 20000) returns the text “alpha”
    Even overwrite D3 with entering ‘900’, then F9 with the same effect. I do not achieve the results you have. Cell reference checking was done 3 times. For your convenience I add the file
    What can I do to get this work?

    Reply

Leave a Comment