Basic Approach
Instead of using Solver to find the values of the Weibull parameters α and β that maximize LL(α,β) as described in Fitting Weibull Parameters via MLE, we can use Newton’s method. The approach is as follows:
Step 0: make an initial guess β0 for the value of β.
Step k+1: assuming that we have an estimate of βk, we define a new estimate βk+1, which should be more accurate, as follows:
We repeat this process until the value of βk converges, at which point we calculate alpha by
Convergence occurs when h(βk) is close to zero or βk ≈ βk+1.
Example
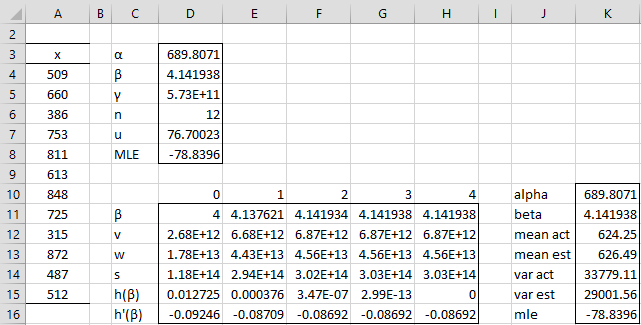
Figure 1 shows how to implement this approach for Example 1 of Fitting Weibull Parameters via MLE.
Figure 1 – Estimating Weibull parameters using Newton’s method
Key formulas from Figure 1 are shown in Figure 2.
| Cell | Item | Formula |
| D3, K10 | =D5^(1/D4) | |
| D4, K11 | =H11 | |
| D5 | =H12/D6 | |
| D6 | =COUNT(A4:A15) | |
| D7 | =SUMPRODUCT(LN(A4:A15)) | |
| D8, K16 | MLE | =D6*(LN(D4)-LN(D5))+(D4-1)*D7-D6 |
| E11 | =D11-D15/D16 | |
| E12 | =SUMPRODUCT($A$4:$A$15^E11) | |
| E13 | =SUMPRODUCT($A$4:$A$15^E11,LN($A$4:$A$15)) | |
| E14 | =SUMPRODUCT($A$4:$A$15^E11,LN($A$4:$A$15)^2) | |
| E15 | =1/E11+$D$7/$D$6-E13/E12 | |
| E16 | =-1/E11^2+(E13/E12)^2-E14/E12 | |
| K12 | actual mean | =AVERAGE(A4:A15) |
| K13 | estimated mean | =K10*EXP(GAMMALN(1+1/K11)) |
| K14 | actual variance | =VAR.S(A4:A15) |
| K15 | est. variance | =K10^2*EXP(GAMMALN(1+2/K11))-K13^2 |
Figure 2 – Key formulas from Figure 1
We have a reasonable level of convergence after only two iterations and by the fourth iteration h(β4) = 0.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Forbes, C., Evans, M., Hastings, N., Peacock, B. (2011) Statistical distribution. Wiley
https://www.academia.edu/49056503/Statistical_distributions
Cohen, A. C. (1965) Maximum likelihood estimation in the Weibull distribution based on complete and on censored samples
https://www.stat.cmu.edu/technometrics/59-69/VOL-07-04/v0704579.pdf
Millard, S. P. (2023) Estimate parameters of a Weibull distribution
https://search.r-project.org/CRAN/refmans/EnvStats/html/eweibull.html
Can you please explain me how you obtain h(beta)
Hi Vincent,
The webpage shows that h(beta) = 1/beta + u/n – w/v. It also shows how to calculate beta, u, n, w and v.
Is there something that is not clear?
Charles
How are the values in D11:D15 obtained? I have a division error for D5. I am not sure of the importance of H12.
DLS
Dennis,
1. You set D11 manually to any reasonable value. I chose the value 4. You can obtain the values in D12:D15 by copying the formulas from E12:E15 into range D12:D15. The formulas in E12:E15 are shown in Figure 2.
2. I don’t know why you would get a division error for D5. The formula in cell D5 uses division by the value n cell D6, which should be 12.
3. The value in cell H12 is not important since convergence has been reached. If convergence had not been reached, then its value would be important since you would need it for the following iteration.
4. You can download the spreadsheet for this example by downloading the Distribution examples workbook from
https://www.real-statistics.com/free-download/real-statistics-examples-workbook/
Charles
Charles,
Eventually I want to be able to use censored data, but I am having trouble getting this spreadsheet to work. 1) Cells D3 and D4 have formulas in them where is the one using MLE does not. 2) Maybe I do not understand how Solver is set up in this instance. 3) To get the iterations, does one simply copy the E11:E16 to more columns? Thanks heaps!
DLS
Hi Dennis,
(1) This is correct. For Solver, D3 and D4 contain the initial values of the parameters. Solver will replace these by optimized values.
For the manual iterative approach shown in Figure 1, D3 and D4 contain formulas, where cell D4 contains the optimized value of beta (and is the same as the value in cell H11. Note that the initial guess for beta is shown in cell D11.
(2) As stated above, in the Solver version, cells D3 and D4 contain the initial values of the parameters. Solver will replace these by optimized values.
(3) Yes, that is correct, you can copy range E11:E16 to more columns. This results in additional iterations.
Charles