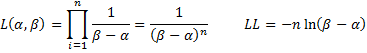Fitting Uniform Parameters via MLE

Basic Concepts

Since the pdf for the uniform distribution on [α, β] is

Uniform distribution pdf

the likelihood estimate for a random sample {x1, …, xn} is

log-likelihood function uniform

provided that all the sample elements are in the interval [α, β] and 0 if not. Suppose that the random sample is in increasing order x1 ≤ …≤ xn. Thus to maximize L we need to ensure that α ≤ x1 ≤ xn ≤ β. But the larger β is the smaller that L is and the smaller α is the smaller L is. Thus to maximize L we need α = x1  and β = xn.

Property

Note that α = x1  and β = xn are biased estimates. If we fix α, we can find an unbiased estimator for β of the uniform distribution in the interval [α, β], as follows.

Property 1: z = α + (n + 1)(xn – α)/n is an unbiased estimator for β, assuming we know α. Similarly, if we fix β, we can find an unbiased estimator for α of the uniform distribution in the interval [α, β], as z = β + (n + 1)(x1 – β)/n.

When α and β are both unknown, we will use x1 + (n + 1)(xn – x1)/n as a quasi-unbiased estimator for β and xn + (n + 1)(x1 – xn)/n as a quasi-unbiased estimator for α. We say “quasi” since neither α nor β is known.

We can also iterate this process as follows. Convergence is quite rapid.

Initialization for uniform distribution

Iteration for uniform distribution

Example

We now repeat Example 1 of Method of Moments: Uniform Distribution using the MLE approach as shown in Figure 1.

Uniform distribution MLE fit

Figure 1 – Fitting a uniform distribution using MLE

The fit using the MLE approach for the uniform distribution is the interval [.004308,99923] as shown in range F7:F8. Range G7:G8 shows a quasi-unbiased version and J7:J8 shows the iterative version.

Note that cell G7 contains the formula =F8+(F4+1)*(F5-F8)/F4 and cell G8 contains the formula =F7+(F4+1)*(F6-F7)/F4.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Forbes, C., Evans, M., Hastings, N., Peacock, B. (2011) Statistical distribution. Wiley
https://www.academia.edu/49056503/Statistical_distributions

Siegrist, K. (2022) Maximum-Likelihood
https://stats.libretexts.org/Bookshelves/Probability_Theory/Probability_Mathematical_Statistics_and_Stochastic_Processes_(Siegrist)/07%3A_Point_Estimation/7.03%3A_Maximum_Likelihood

Millard, S. P. (2023) Estimate parameters of a uniform distribution
https://search.r-project.org/CRAN/refmans/EnvStats/html/eunif.html

Leave a Comment